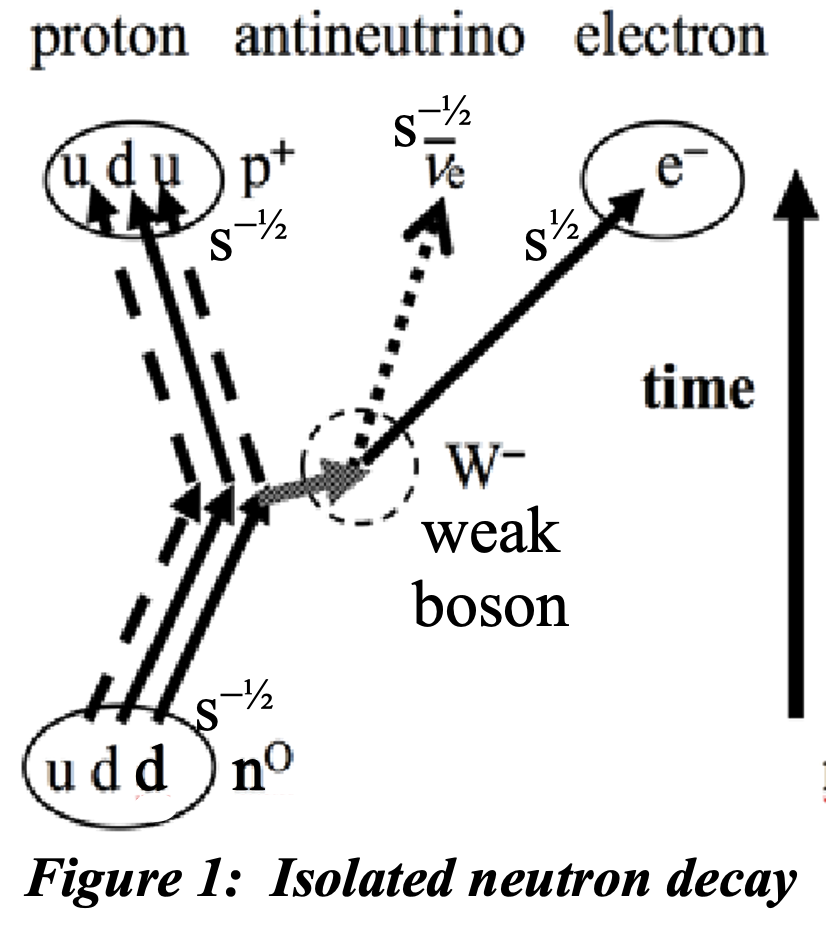
An isolated neutron no will decay in about 881.5 seconds into a proton p+, an electron e–, and an antineutrino 𝜈. This is shown in figure 1, where the up quark u+2/3 and down quark d–1/3 are the constituent lower level particles of the neutron and proton, the electron is presumed to have no such lower level constituents. All these pre- and post-reaction particles have spin s±½, with the amount of spin given in the superscript. The charges are indicated as superscripts as well and are in units of electronic (electron’s) charge.
The free neutron decay process is described as follows:
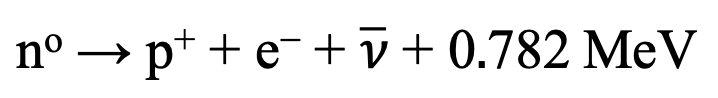
The 0.782 MeV of energy released (1.253 x 10-6 erg) in the process corresponds to the difference in mass of the neutron (1.675 x 10-24 gm) and the sum of the masses of the products of the neutron decay, the proton (1.6726 x 10-24 gm) plus the electron (9.109 x 10-28 gm). This mass difference is 1.392 x 10-27 gm. Whether an additional gamma ray is emitted during the weak interactions with atomic nuclei also involved, depends on specific the circumstances of whether the newly formed proton is in an excited state that will then emit a gamma ray. Inclusion of gamma ray emission adds complexity to the otherwise simpler dynamics of the decay process. But that additional complexity is a separate process that need not have been precipitated by the neutron decay process.
In figure 1 slope of arrows indicate right-left movements as functions of time – the electron proceeding more rapidly than the proton because of its lighter mass. The process conserves the total energy and momentum. So the total energy of the neutron incorporating both rest mass and kinetic aspects due to its motion. This is transferred into the same dual aspects of energy in the proton and electron. Charge and particle spin – related to angular momentum – is also preserved in the particle interaction. But there’s a bit of alchemy required involving transmutation of a down quark into an up quark with an extremely short-lived “weak boson” W– that carries off the charge difference of -1. Having performed its magic the weak boson quickly decays into an electron and an antineutrino as shown. What is not shown in this, or similar diagrams is the accepted understanding that in addition to the quarks, hadrons, i.e., neutrons and protons (or any particle made up of two or more quarks) have less than two percent of their mass vested in the quarks; gluons that are exchange particles are responsible for maintaining both the association and separation of the quarks via the ‘strong force’, since charged quarks would otherwise collapse into a singularity under assuming the electrostatic force on point particles.
The determination of a role for the antineutrino is made by solving the conservation equations for momentum and energy of the neutron, proton and electron. In addition to energy and momentum, each particle’s electric charge and spin are also preserved. Spin conservation is the primary problem that the neutrino and its anti-particle were designed to solve but that required the momentary miracle of the W–. Since all the subatomic particles in figure 1 exhibit spin ± ½, without the anti-neutrino, the spin of a ±½ neutron would decay into a total spin of 0 or 1, and spin would not be conserved. An associated problem is that there is evidence of a variable amount of extra energy and momentum that is not accounted by the proton and electron dynamics. And while measuring the energy and momentum of decay products in free neutron decay could, in theory, determine the mass of the antineutrino, the practical challenges associated with the tiny-required neutrino mass, measurement precision, and the need to control systematic uncertainties make this task extremely difficult in practice and there is no conclusive evidence that the antineutrino has any mass at all. That’s the party line.
In our next installment on this blog we will address an alternative that addresses the effects
Leave a Reply