In the previous post we addressed the standard model(s)’s explanation of the transition from a universe comprised of a quark soup to the universe we observe today. That previous approach involves transmutation of a down quark into an up quark and synchronized ex nihilo creation of an electron and a neutrino. The rationale is to salvage the conservation of energy, charge, and spin in accounting for neutron decay. That rationale is essential, but it the implementation is poor. And there are even more major issues that have been ignored that need to be addressed in explaining the transition from a quark soup to the subatomic particles that comprise our universe with its predominantly hydrogenous plasma.
To begin, whatever happened to Lucretius’s dream of an atomic theory of matter where all that we see is comprised of a set of immutable particles? Is it naïve to cling to the notion that at some level of existence immutable particles exist whose combinations constitute the observable universe? The up and down quarks had seemed a last vestige of that victory over alchemy; but are they? Let’s analyze what wrong with the currently accepted concept, and in so doing determine an appropriate alternative explanation.
This is the accepted depiction of the neutron decay process that completes the transition from quark soup to whatever we have today:
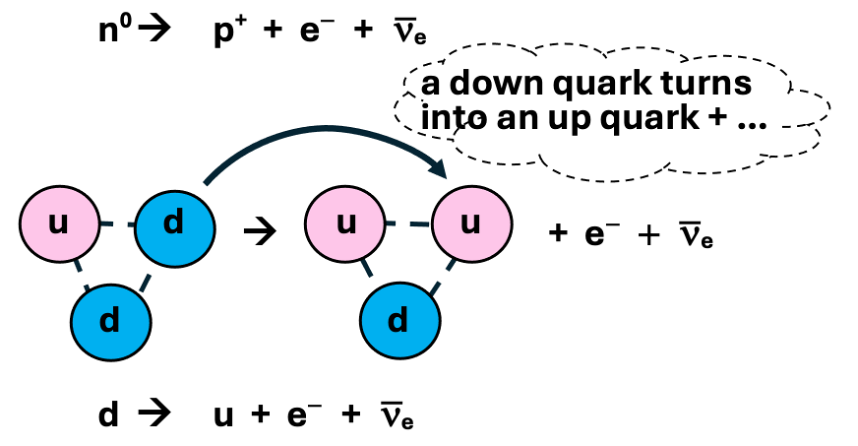
List of problems with this picture:
#1 mass
The masses that have been assigned to the constituent quarks of the neutron and proton are a very minor portion of the mass of the subatomic particles themselves, i.e., only about 1%. Why? Because the vast majority of the mass is tied up in the undepicted gluons that would be required to provide adherence and avoid singularities of quark electric charges. The gluon is the responsible particle for enforcing the ‘strong force’ that overwhelms the electrostatic forces between the quarks. The mass of the gluon is not depicted.
#2 the strong force
The strong force is required because the archaic notion of mathematical ‘point’ charges that are not distributed throughout space. Forces between point charges would become infinite as their separation approaches zero. Tremendous forces would be required to house the point charges of quarks within the spatial dimension of a subatomic particle.
#3 charge
The one-third of a negative electronic unit of charge invested the down quark somehow spawns the two-thirds of a positive electronic unit of charge invested the up quark and a full negative unit of electronic charge for the electron. Where do these properties of a down quark and the energy to complete that feat come from? Not the strong force because the proton would require more of the strong force to separate the stronger electronic charges of its up quarks.
#4 particle immutability
Particle immutability is at the heart of the atomic theory of matter. Certainly the Periodic table of elements addresses the issue, but then, since the subatomic particles themselves are comprised of another level of particles, at some level there must be fundamental particles that can’t be ‘split’. For ordinary matter the up and down quarks should be it, but traditional particle theory does not support that notion. Ratios of numbers of up and down quarks changes according to current consensus but not the alternative explained here.

#5 conservation of spin
The quarks all possess half-integral spin as, therefore, do the neutron and proton. The electron also possesses half-integral spin. The neutrino is thus a required afterthought to conserve spin.
#6 conservation of energy
Whatever energy exists in the neutron assuming the decay process is being considered in the rest frame of the neutron, must be present in the rest mass energies and kinetic energy of the resulting particles. The proton and electron masses and kinetic energies don’t add up to the rest energy of the neutron, which becomes another rationale for the existence of the neutrino.
What we know for certain
What we know experimentally of the neutron decay process is the properties of the proton and electron products. All else is conjecture. The validity of the conjectures that explain the behavior of the two products relies on consistency. For example, the complementary charges of the proton and electron, their receding velocities from their point of origin, and their curvature in a magnetic field. From this data their total rest mass and kinetic energies can be inferred to deviate in a continuous spectrum from that of the rest mass energy of the neutron. So there must be something unseen within the decaying neutron or an additional neutral product. We opt for the former involving a colliding bipartite neutron.
Particle detection is a technology with considerable history, starting with bubble and cloud chambers in strong magnetic fields; now usually employing sophisticated pixel detectors as in experiments at CERN.

problem and solution to the assumed quark charge arrangements
The before and after charges balance, but to balance the mass has required the larger of the quark charges to have the least mass. This is complicated by the assumption that a strong force is required to make this scheme work and ultimately becomes the primary determinate of mass. But a separate ‘strong’ force is required because charge has always been presumed to defy continuous distribution in space.
What we know about the neutron is that it is neutral and its inferred mass, and as such it does not show up on particle detectors. So, we know that it must contain twice as many down quarks as up quarks, depending on the masses of the up and down quarks. Multiple confined quarks cannot share the same one of the three ‘colors’, so particles have been assumed to possess no more than three quarks. But a three-quark particle will possess a dipole moment that attracts the opposite polarity. So two three-quark neutrons will have an affinity for each other resulting in a fatal union with the four down quarks forcing the odd one out with the proton structure and a three-down quark unit electronic charge remainder.

The envisioned quark soup is comprised of twice as many down quarks as up quarks to maintain an overall neutrality. And although the standard model envisions the primordial quarks as fundamental, it ends up with the current universe possessing a substantially different ratio of the numbers of the up and down quarks. This is the starting point for the alternative, i.e., the conservation of number of up and down quarks.
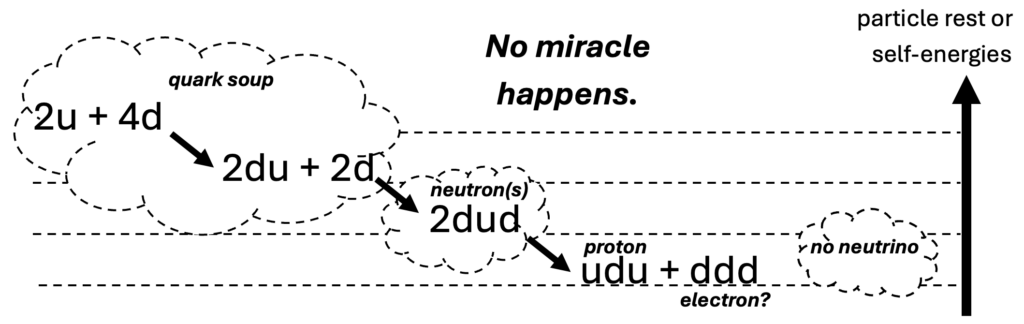
So how does this differ from the accepted miraculous explanation? Well, let’s look at the differences in the associated equations:
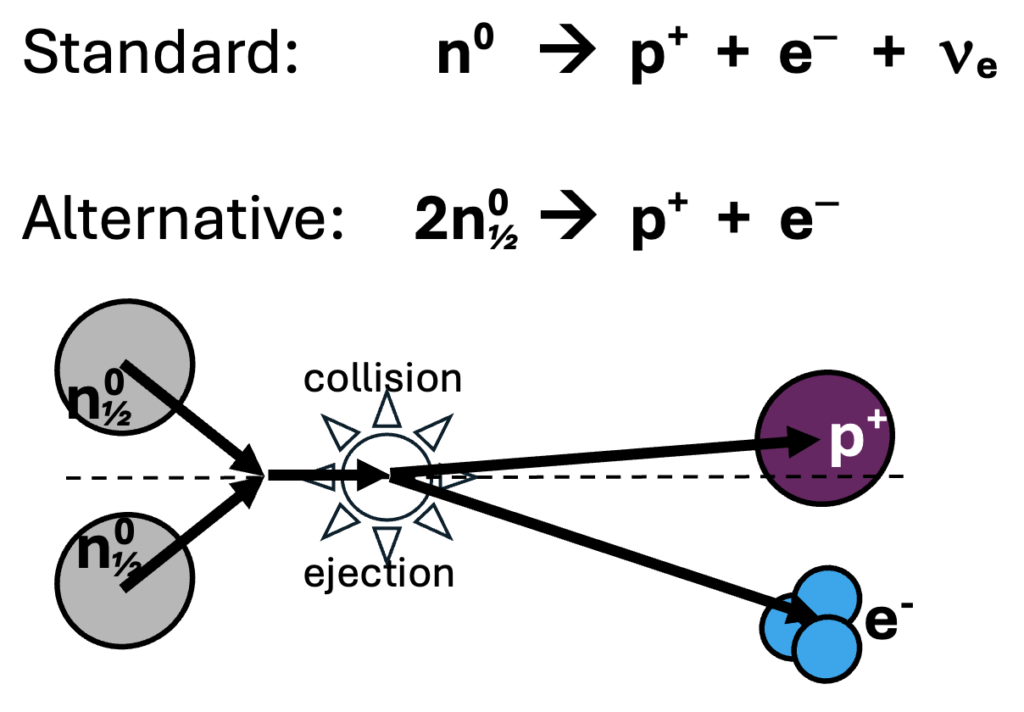
The bipartite neutrons are paired in as much as their single up quarks must have a different color to meet chromodynamic constraints on the resulting proton. So when a neutron pair are ejected from an elemental nucleus, ‘decay’ is predictable. There will always be one of two down quarks with the same color that will join the compatible up quarks in the proton. The resulting energy available to the proton and electron will vary continuously as observed and will have an upper limit because the closing velocity of the two bipartite neutrons can never exceed c and therefore the energy contributed to the products will vary:
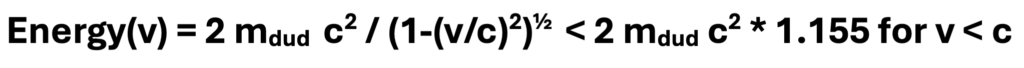
This will result in the observed continuous spectrum of beta particle energies.
Of course there are questions with regard to the implied masses of the quarks, but we must first address the elephant in the room – the gluon. Why is it here? How can we get rid of it?
problem and solution to the assumed quark charge distributions
The gluon has been perceived as required to deal with what would otherwise result in singularities of quarks of similar charge colliding with infinite force. Quarks of dissimilar charge would similarly avoid each other violently – not a friendly environment within the restricted confines of a subatomic particle. The problem is, of course, the time-honored assumption of point charges. The Dirac delta function was invented as a means of dealing with this problem. A Dirac delta function is a function that exhibits a very confined region with a non-zero value in the limit as the width of this region goes to zero. There are many functions that provide this functionality with the width sufficiently small to approximate a point charge distribution. Quantum wave functionality has provided a smearing out of the position of an otherwise ‘point’ particle, but a central question remains: Are units of charge restricted to a single point? The answer is: Obviously not!
The potential and the distribution of charge are inextricably linked by the Poisson equation for both electrostatics and gravitation. Solutions of the equation depend on establishing boundary conditions on the domain for which the solution applies. These conditions specify reasonable values of parameters at all boundaries. I open space the values must vanish at an infinite distance from the center of the charge. For a point charge at the origin and no charge elsewhere, the solution is the inverse square law force. However, the origin should also be considered a boundary. When that is done for a total charge of Q, solution for the charge density is the following:
r(r) = Q e-a/r / r4, where a is constant of integration determined by the boundary conditions.
The force field at a distance r from the center becomes:
E(r) = q(r)/r2, where q(r) = Q e-a/r, amount of charge circumscribed in the sphere of radius r.
The potential of the charge distribution is defined such that its gradient is the negative of the force field. In this case we have:
V(r) = Q ( 1 – q(r) ) / a
The total self-energy of such a distribution is:
Energy = Q2 / 2 a = M c2
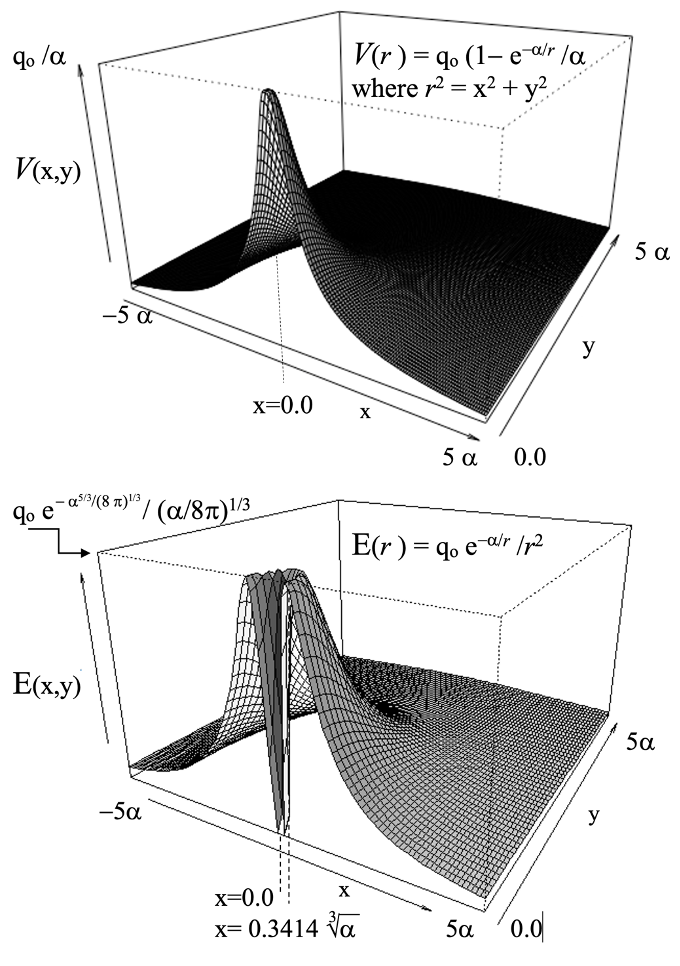
Thus, the mass of the distribution is determined by the total charge of the distribution and the inverse of its variance. The mass of the individual quarks is not relevant to associated masses of subatomic particles because it no longer requires the tremendous strong force to encapsulate the quarks. There is no singularities and the electrostatic forces between closely held quarks diminishes to zero at the origin.
applying quark charge distributions to subatomic particles
So, let us consider interactions between the up and down quarks for the traditional and the alternative quark fields. For an inverse square law force, separated charged particles would attract or repel each other with increasing force as their separation is reduced—the amount increases to infinity as the separation goes to zero. In the alternative view involving the Poisson distribution, the inverse square law proportionality is ameliorated as the separation is reduced to the vicinity of the deviation factor α, and this reduces the force to zero (rather than infinity) at zero separation. There is no singularity. This fact has significant ramifications with regard to the supposed substructure of the subatomic particles. In the following figure, linear neutron and proton quark substructures are shown. Implications of the differences in the traditional inverse square and alternative force fields are immediately obvious.

In the conventional (C) and alternative proper Poisson (P) electric field strengths (Eu or Ed), divided by the mutual inverse-square factor, realized at the location of the central quark in the case of the proton are determined as follows:
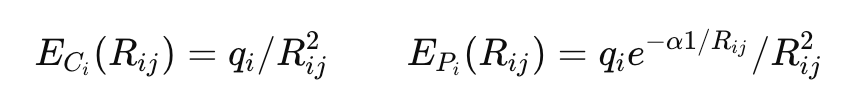
We include a ‘C’ in the subscript for the classical field strength and a ‘P’ for the Poisson field strength. By eliminating the inverse square factor, all classical plots are horizontal.
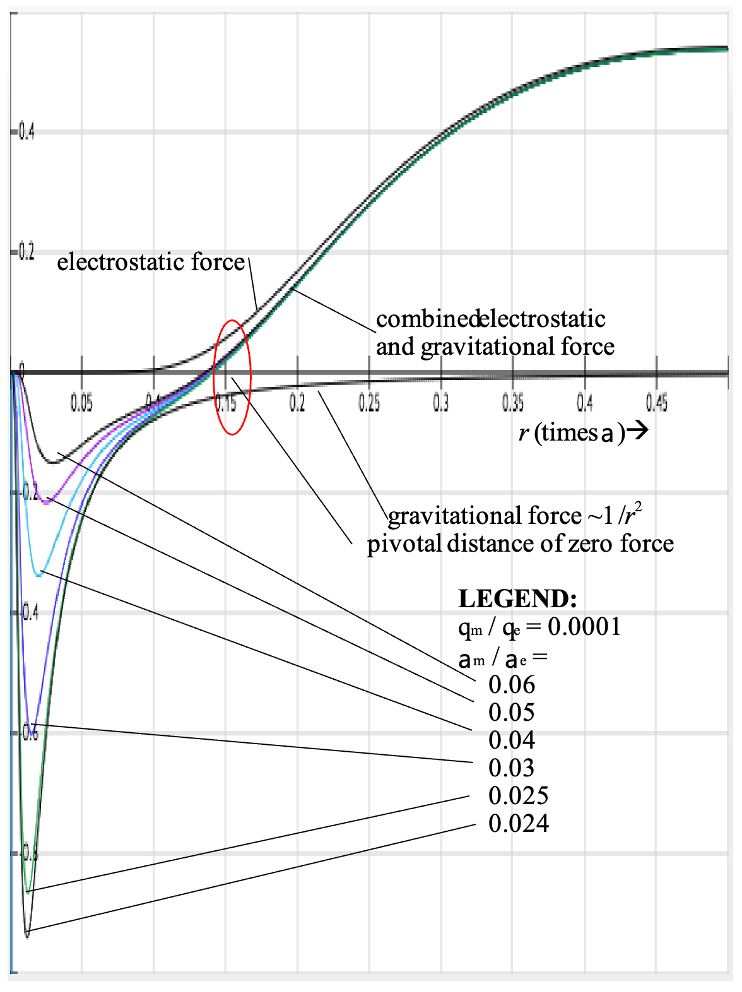
The electric binding/repelling force of quark combinations according to the traditional view would be as shown by the blue line in the figure below. Stable non-juxtaposed combinations that would otherwise constitute singularities would require an extraneous force (the ‘strong force’ attributed to ‘gluons’) to enforce subatomic spatial separation. However, the Poisson charge distribution accommodates stable separation of the quarks in subatomic particles without introducing gluons. In this figure the regions of attractive and repulsive forces as a function of the separation R of each the two down quarks from the central up quark in the proton are illustrated. The inverse square factor that applies to both the traditional and alternative force fields has been cancelled for the comparison.


a role for gravity
Gravity also plays a role with the similar but negative energy functionality resulting from the similar Poisson equation such that when quarks of like sign are brought into close proximity it forces them to adhere rather than repel each other. It’s like the buttons on the Legos that snaps two of them securely together. Thus, a three down quark electric charge distribution can become one particle with down quark distribution features, but with triple the charge. There is R-G-B chromatic stability of three quarks and the half-integral spin characteristic required of a lepton.
problem and solution of the unobserved particles
The gluon was invented to implement the ‘strong’ force to bind quarks together and not too tightly. With the Poisson solution rather than simplified inverse square law associated with the charge and mass distributions of the quarks, all that is unnecessary.
The neutrinos were invented to explain why the beta spectrum is continuous rather than discrete and to provide a half-integral spin that a single three-quark neutron decay does not provide. In the alternative the product energies vary because the bipartite neutron collision energy varies, and spin balance is unchanged since the number of quarks is unchanged throughout the process.
completing the picture
We’ve shown some functions and equations that provide a general picture of the transition of particulate matter from one form to another in terms of a set of immutable fundamental particles that never change despite their use in various subatomic structures. There’s no longer any hocus pocus. But how well do the numbers fit?
The assignment of the mass, charge, and spin of the constituent quarks derive from those same properties of the neutron, proton, and electron without the distraction of the gluon and neutrino. These masses are:
neutron: Mn 1.675 x 10-24 grams or 939.6 MeV
proton: Mp 1.673 x 10-24 grams or 938.8 MeV
electron: Me 9.109 x 10-28 grams or 0.511 MeV
Disregarding dynamic and binding energies at the highest level of approximation, we have the following equations for quark masses Mu and Md:
Me = 3 Md
Mp = 2 Mu + Md
Mn = 2 Md +Mu
From the mass of the electron we obtain:
Md = 3 x 9.109 x 10-28 = 3.036 x 10-28 grams or 0.1703 MeV
From the masses of the proton and the electron we obtain:
Mu = ( 1.673 x 10-24 – 3.036 x 10-28 ) / 2 = 8.36 x 10-25 grams or 468.9 MeV
Or from the mass of the neutron and the electron we obtain:
Mu = ( 1.675 x 10-24 – 2 x 3.036 x 10-28 ) / 2 = 8.37 x 10-25 grams or 469.5 MeV
So let’s accept Mu = 8.365 x 10-25 grams or 469.2 MeV
From these mass values and the quark charges we can determine the associated variances in the up and down quark charge distributions:
au = Qu2 / ( Mu c2 ) = ( 2/3 x 4.8 x 10-10 )2 / ( 2 x 8.365 x 10-25 x ( 3 x 10-10 )2 ) = 6.80 x 10-17 cm
ad = Qd2 / ( Md c2 ) = ( 1/3 x 4.8 x 10-10 )2 / ( 2 x 3.036 x 10-28 x ( 3 x 10-10 )2 ) = 4.68 x 10-14 cm
And that as they say is that.
Leave a Reply