Why exchanging photons differs from playing catch with a ball

In our previous post we illustrated with baseball players how mediating the interactions between particulate matter by exchanging particles rather than by simple elastic collisions does not in itself address the reversibility vs irreversibility issue.

If we add a couple of constraints to the exchange of energy and momentum depicted as tossing a baseball back and forth between ball players on skate boards, the situation becomes totally different. See figure below. 

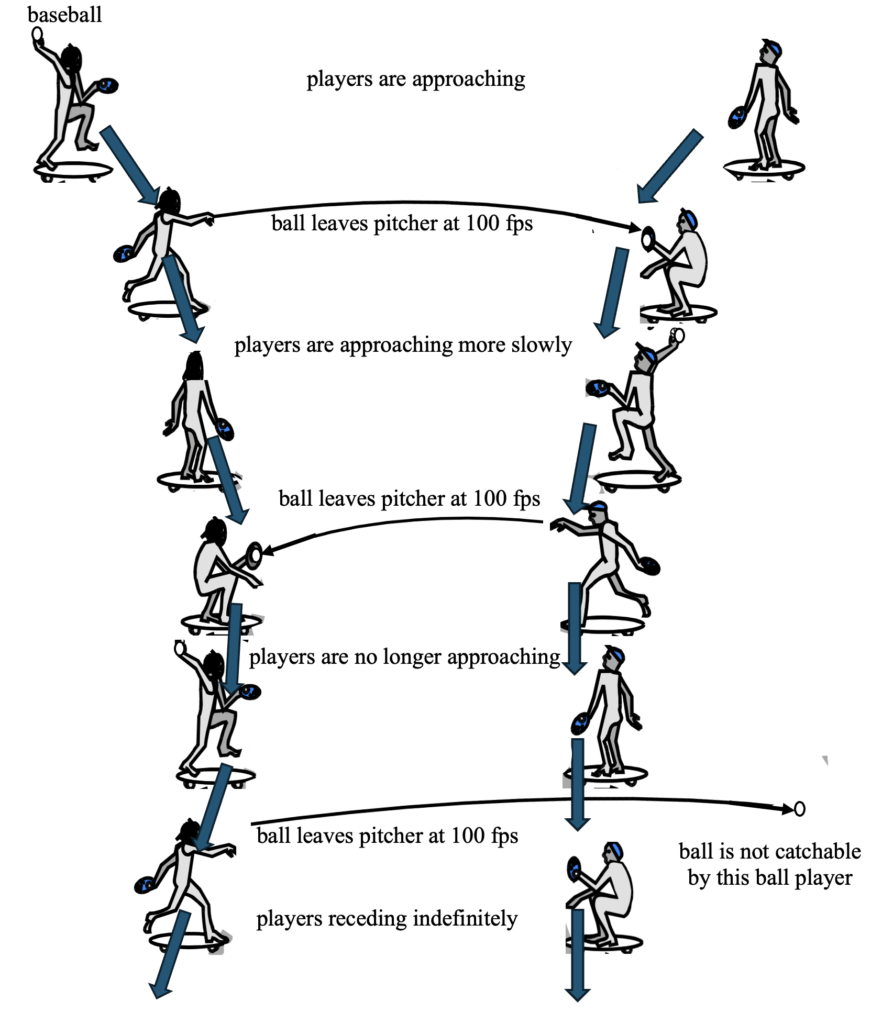
mediation with a ball velocity constraint

Suppose that each player can only throw the ball at precisely 100 feet per second.  Further, let us suppose that each player can catch a ball if it is traveling at 100 feet per second or greater but not if it is traveling more slowly.  They begin at some separation with approaching relative velocity.  Player 1 throws the ball at 100 feet per second relative to himself, but his recoil velocity reduces this velocity slightly for a relatively stationary catcher.  However, if player 2 is approaching at a relative velocity greater than this recoil velocity he can catch the ball, recoiling slightly as he does.  This exchange can continue until the sum of their recoil velocities brings them to a relative standstill or to actually receding slightly.  At this point it is game over; the ball has become uncatchable because the recoil velocity will reduce the ball’s speed for the catcher below 100 feet per second.  These rules of engagement make the interactions irreversible.  By reversing all velocities, we have a situation with a receding relative velocity rather than an approaching one, rendering the ball uncatchable in every case.

The very existence of radiation requires non-elastic collisions of particles.  A hydrogen atom, for example, that collides with another hydrogen atom at high enough speed will ‘knock off’ an electron or at least ‘jar it loose’, such that it absorbs enough energy to bump it up to a higher internal energy level.  In either case some of the excess relative-velocity-related kinetic energy is freed up in loosening attachment of the oppositely charged electron and proton.  These will eventually collapse back into lower energy states releasing radiant energy in the process.  Or, two colliding atoms will bind together upon contact sharing their electrons to form a stable molecule of H₂, also releasing energy.  In all such inelastic collisions, the released energy will be in the form of radiation, a different form of energy altogether from the rest mass and kinetic energy of particles.  We know it is of a ‘different kind’ because the relationships between conservation laws of energy and momentum differ for photons of radiation and for particles. So let’s explore this difference:

The energy and momentum of a particle are not directly proportional to each other.  The energy of a photon of radiation on the other hand is directly proportional to an analogous expression for momentum associated with that photon. There are dramatic consequences that derive from this very essential difference between the rather flexible energy-momentum relationship of particulate components of a gas and the similar (but more constrained) energy-momentum relationship of radiation associated with that very same gas. The disparity in these relationships is a well-known fact.  But those who have tackled related issues have typically continued to be unaccountably oblivious to the role of this essential difference in the context of analyses employed by both Boltzmann (who was understandably unaware of it altogether) and Einstein in developing their respective models of particles and radiation. Incompatibility of energy and momentum relationships introduces stringent additional constraints on conservation principles employed in determining the effects of interactions within thermodynamic systems.

In analyzing these interactions using classical Newtonian mechanics the applicable functional relationship between the conserved kinetic energy Ek(p) and the momentum p of a particle exhibits the following nonlinear (squared) relationship,

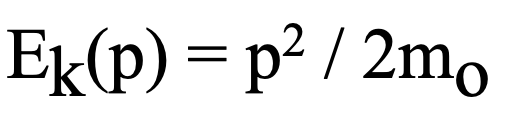
This is shown as the dotted line in figure 3 where m_o is the constant (rest) mass of the submicroscopic particle independent of the particle’s velocity.

Einstein’s relativity theory demands a revision of these classical formulas for particulate matter with the mass of a particle now dependent on its relative velocity. The relevant relativistic equations become respectively:

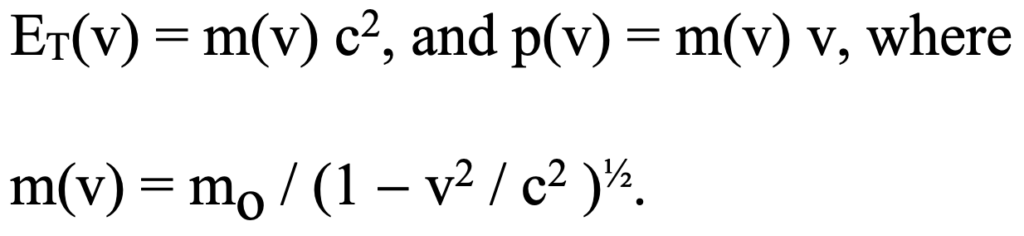
The dynamic mass m(v) depends on its relative motion with respect to the observer for whom the equations apply.  The universal constant speed of light is c.  So that the kinetic energy of a particle is:

It is the kinetic portion of the total energy of the particle that results when one subtracts the ‘rest mass energy’ E_rm from the total.  Other than for small velocities, we no longer have the direct square relationship between momentum and kinetic energy. The relationship remains nonlinear, but now it is a little more complicated. As can be easily seen, this functionality becomes closer and closer to the linear relationship exhibited by radiation as the relative velocity of a particle becomes closer and closer to that of the speed of light. This is shown as the dark solid line in the figure below.

The quantum behavior of photons of electromagnetic radiation on the other hand is constrained by an energy-to-momentum relationship that is strictly linear. This is in part because the rest mass of a photon is zero and also because of the wavelength dependence exhibited in the quantum theory of radiation where the commensurate energy and momentum parameters are given by:

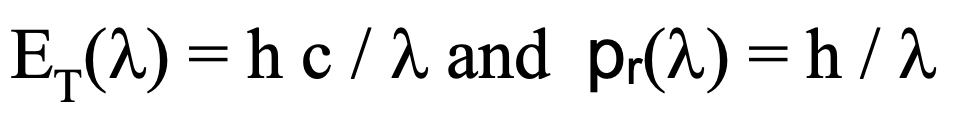
Here lambda is the wavelength of the radiation and h is Plank’s constant. Notice that the frequency n of such radiation is given by nu  = c / lambda.  Thus, photons (unlike their particulate component counterparts) are constrained by a precisely articulated proportionality such that:

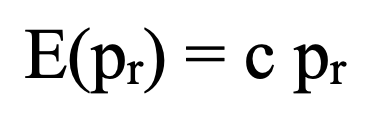
This is shown by a light solid line superimposed on the plots of the preceding figure. Even for the proper relativistic equations, this differs significantly from the situation that applies to particulate components although, as illustrated, the differences do become much less at extremely high energies.

These differences between particulate and radiation exchanges are primarily understood as relativistic effects of Doppler and mass-energy relations. But the irreversibility at the submicroscopic level of our existence that accounts for entropy require an understanding of the quantum effects of radiation that we will discuss in the next post. The speed constraint on baseballs in the first figure above is imposed by a combination of quantum and relativistic aspects of the interaction as we will demonstrate.