So there are some dumb arguments that we need to avoid when we discuss irreversibility and entropy. We need to start at the beginning with a discussion of the interactions of submicroscopic particles such as molecules and the atoms of which all (non-mysterious ‘dark’) matter is comprised. We have already (in a previous post in this blog) done away with arguments that concluded that elastic collisions of subatomic particles can somehow result in irreversibility. They can’t. Nor could mediated non-elastic interactions be irreversible if effected by the exchange of material particles of any kind possessing rest mass.
We are left with a question: Can interaction between particles mediated by electromagnetic radiation result in the irreversibility and entropy that is observed at the macroscopic level of reality? In this regard it is significant that particles possess energy and momentum differently than the conserved quantities that are possessed by radiation as illustrated in an earlier post. If irreversibility enters at the submicroscopic level of reality, as reductionists like many scientists insist, myself among them, then entropy enters via the inelastic ‘collisions’ involving radiation exchanged between particles. Let’s investigate how both energy and momentum are conserved in these exchanges even though their proportionality is so different for the participants.
It should not come as a surprise that explaining entropy is a non-trivial exercise. So I have divided the remainder of the task into two discussions. The first being the proof that submicroscopic interactions are not reversible. Because of relativistic and quantum effects, none of them are.
The impact of Einstein’s relativity
Prior to the previous century, it was accepted that if two objects were in relative motion, one emitting radiation toward the other, there would be no restriction to the transmission other than a Doppler shift in its frequency (energy). Newton’s corpuscular theory of light did nothing to change that. So if object #1 is moving to the left on a path from A to B, its relative motion v can be characterized as having a radial (receding or approaching) velocity vr and a transverse (tangential) velocity vt as shown below.
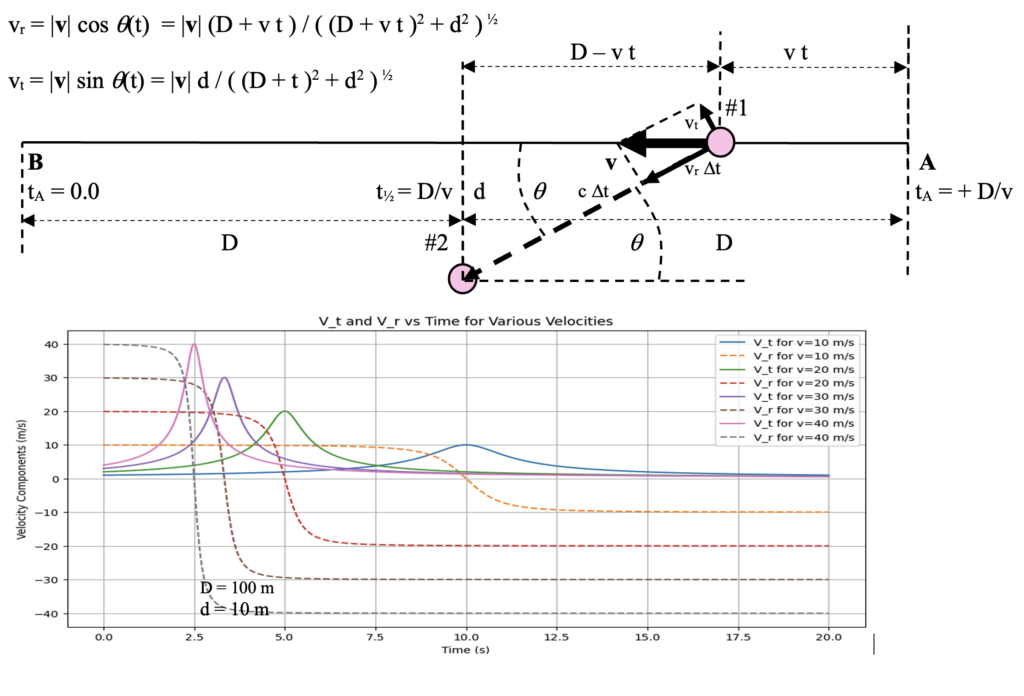
According to classical theory, light from a source on object #1 would reach object #2 no matter where object #1 was situated or how fast it was traveling along the path at the moment light is emitted. In the classical Galilean theory of relativity, the velocity of light transmission would be altered by the relative motion. The Doppler shift in frequency (and wavelength) changes over time as object #1 travels along the path commensurably with the radial velocity at each point in time. The classical Doppler formula specified that frequency and wavelength would be modified in accordance with the following formulas:
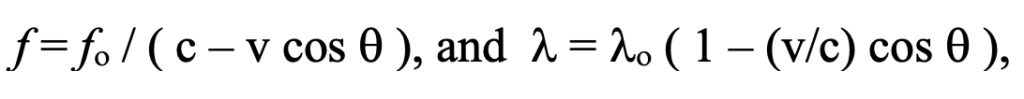
Where fo is the symbol used for frequency of the emitted light, f is the Doppler-shifted frequency of the light received at object #2, v is the velocity of object #1 along the path from A to B, c is the speed of light through a vacuum—relative to object #1 in non-relativistic physics, lo = c / fo is the wavelength of a photon of emitted light, and l is the wavelength of the Doppler-shifted light received at object #2.
The velocity of object #1 includes only the ‘radial’ velocity component, vr = v cos q, directed directly at or away from object #2 and the ‘transverse’ component, vt that is at a right angle to the direction to object #2 is completely ignored. This functionality is illustrated by the dashed lines in the figure below.
In classical physics of the 19th century it was assumed that the speed of the light emitted at object #1 and detected at object #2 would be the vector addition of the velocity of the source and a constant value c determined by properties of the supposed ether.
relativistic phenomena involved in Doppler shifts
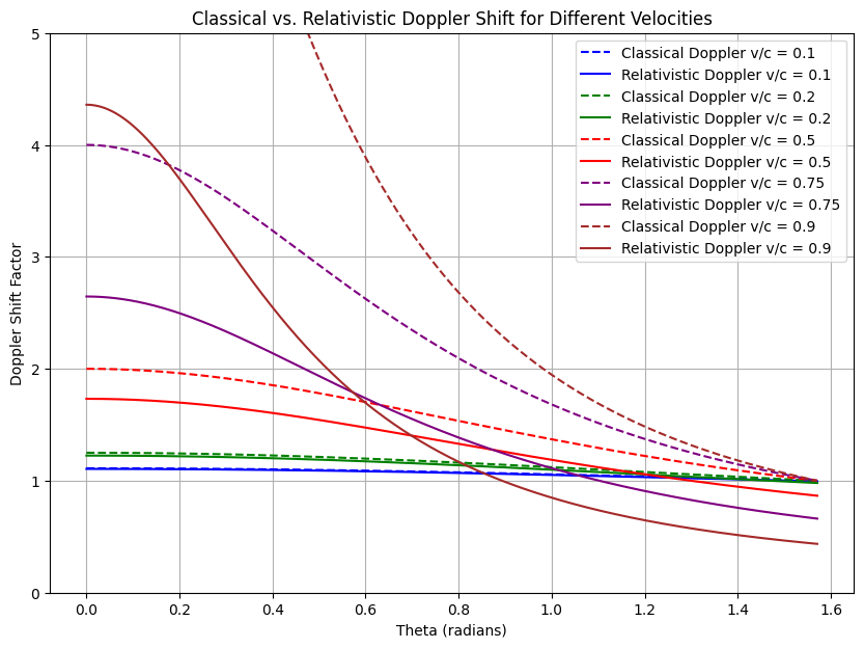
With the introduction of Einstein’s special theory of relativity the expectations for the Doppler Effect on radiation changed. Einstein’s second postulate, that the velocity of light is the same for all observers (and thus for all absorbers of radiation) independent of their relative motion with regard to the source of that radiation in a vacuum, required a different explanation of the observed phenomena. That explanation, like most of what follows in Einstein’s theory of relativity can be simply derived from the applicable Lorentz transformation equations. Thus a revised Doppler formula came into being:

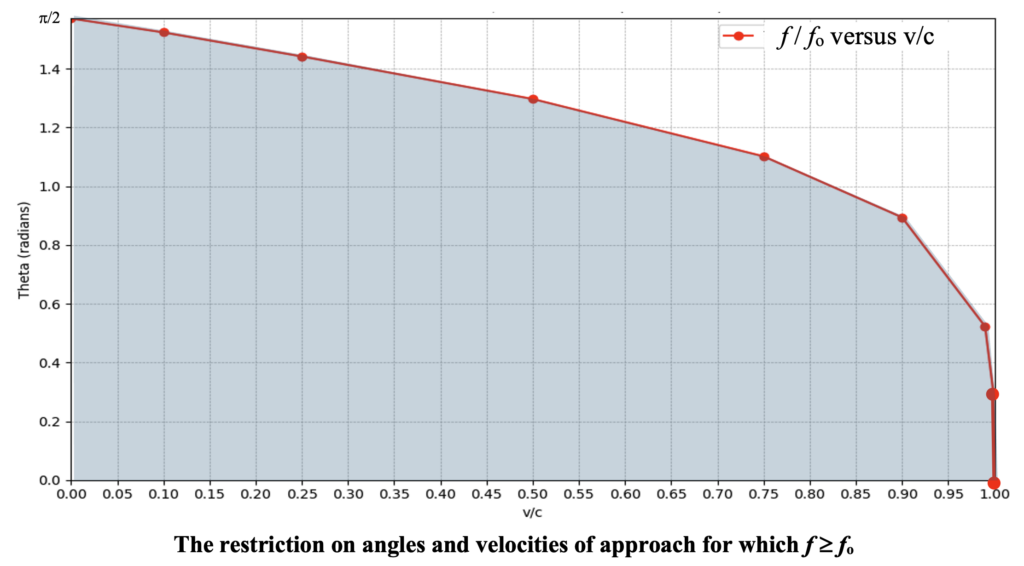
This gamma factor contributes very little to the effect unless the relative velocity v of the source with regard to the observer is significant with respect to the speed of light, c; this is a caveat that isn’t usually required on a single interaction. However, when relative velocities are appreciable the effect of the gamma factor can be an observable fact. Refer to the figure above where the Doppler shift factor is illustrated for both the classical and relativistic formulas in the case of v/c = 0.1, 0.2, 0.5, 0.75, and 0.9.
quantum phenomena involved in energy transitions
The energy constraint involves only discrete changes in the rest mass energy of submicroscopic particles associated with binding energy levels of electrons about the nucleus of atoms. In hydrogen gas for example, photons with frequencies in the vicinity of the hydrogen atomic spectral lines of the element are swallowed up in transitioning atoms to a higher energy level. This phenomenon, perhaps best described by ‘the Bohr atom’, involves quantum energy transitions of electrons captured in the coulomb potential energy well of the proton nucleus of the hydrogen atom. In this conceptualization shown in the figure below, bound electrons are restricted to allowed orbital situations for which their energies are limited to specific quantum energy levels defined by the following equation:
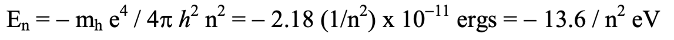
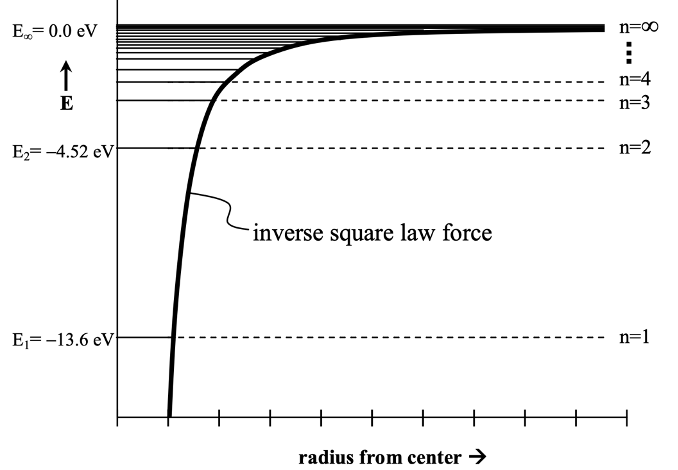
Hydrogen emission/absorption line series
Where n is an integer, n = 1, 2, 3,… , mh =1.6726×10-24 gm is the mass of the hydrogen atom, and e is the electronic charge. The minus sign has to do with these energies being associated with bound states in the potential energy ‘well’. We also have Planck’s constant, h = 6.626 x 10-27 erg seconds. In addition there a conversion constant is required to convert energy in ergs to electron volts, where 1 eV = 1. 60 x 10-12 ergs.
The important Lyman energy transition series is labeled in the figure below along with the Balmer and Paschen series that play somewhat lesser roles in usual discussions. If the hydrogen atom is in its lowest energy state E1 with a single electron in its lowest ‘orbit’, the atom can transition to the next higher energy state E2 by absorbing a photon whose energy is given by,
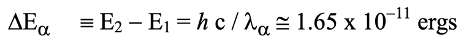
This Principle of Detailed Dynamic Balance resulting from Einstein’s work involves discrete energy transitions between and among the various energy levels of constituent atoms being precisely constrained to continuously maintain conservation. Thus, even though one atom or molecule can emit radiation to transition from say a state E10 down to E7, for example, this energy transition cannot be precisely balanced by three atoms or molecules, each absorbing portions of the photon to produce the following transitions: E7 to E8, E8 to E9, and E9 to E10, in three such molecules respectively or in three separate stages of a single molecule. This restriction applies in both directions. Photons are indivisible. The conservation of energy is maintained on each and every transition indivisibly as shown in the following figure. Potential energy wells of two atoms and their quantized energy levels are shown. As shown, the exchange would seem to accommodate reversibility, but the exchange would actually require the two atoms to be approaching to compensate for frequency (energy) losses due to recoil
Hydrogen emission/absorption line series
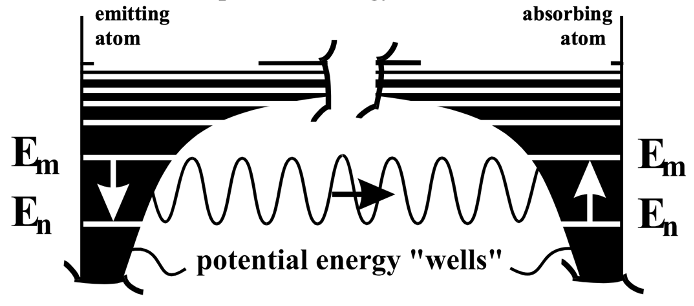
The precise potential energy balance of exchanges of quantized energy without addressing the conservation of momenta
merging the effects of relativity and quantum mechanics.
There is a collaborative impact of the two major theories of the century-old ‘modern’ physics on the interaction of submicroscopic particles. Not only are the frequencies of mediated interaction constrained to being greater than or equal to the transition to the next level in the absorbing atom, with excess above that adding to the recoil, but relativistic Doppler effects further restrict the domain of angles from which an atom can receive radiation at or above a given frequency. This is because of the transverse velocity component which increases wavelength even where there is no radial velocity. Thus, the incident angle at which the frequency f is equal to or greater than the fo that was emitted is further reduced. This restricts pairing selection further than just that the pair are approaching each other. And in all cases must be approaching to interact and thus reversing velocities – the essence of reversibility – is precluded.
We will see how this affects thermalization and entropy in the next post.
Leave a Reply