To coordinate observation between coincident but relatively moving observers, one must translate the coordinates of the observed event to those of the other observer. Each observer is associated with a reference frame constituted by a set of mutually orthogonal coordinate axes in space and a time interval to the observed event. Thus, a coordinate transformation involving a set of equations is required. The traditional mathematical approach to coordinate transformation involves a tensor (or matrix) construct which, when multiplied times a vector of values in one coordinate system yields the associated vector of value in the other, as for example:
rm = T mn rn ,
where T mn is the transformation. This tensor notation can be interpreted using matrix notation as follows for the specific case of what I call the ‘observation’ transformation:
Notice that the index m (rows) is a sum over n (columns) in the transformation matrix O mn above that differs from the corresponding Lorentz transformation L mn by having incorporated a leading scalar factor alpha (a) in this particular case. This difference within the general class of observational transformations is most easily characterized as:
O mn = a L mn
The preference for the former is that it takes into account the non-orthogonality of the ‘other’ observer’s coordinate axes when observed in ‘this’ reference frame.
What is the spacetime interval?
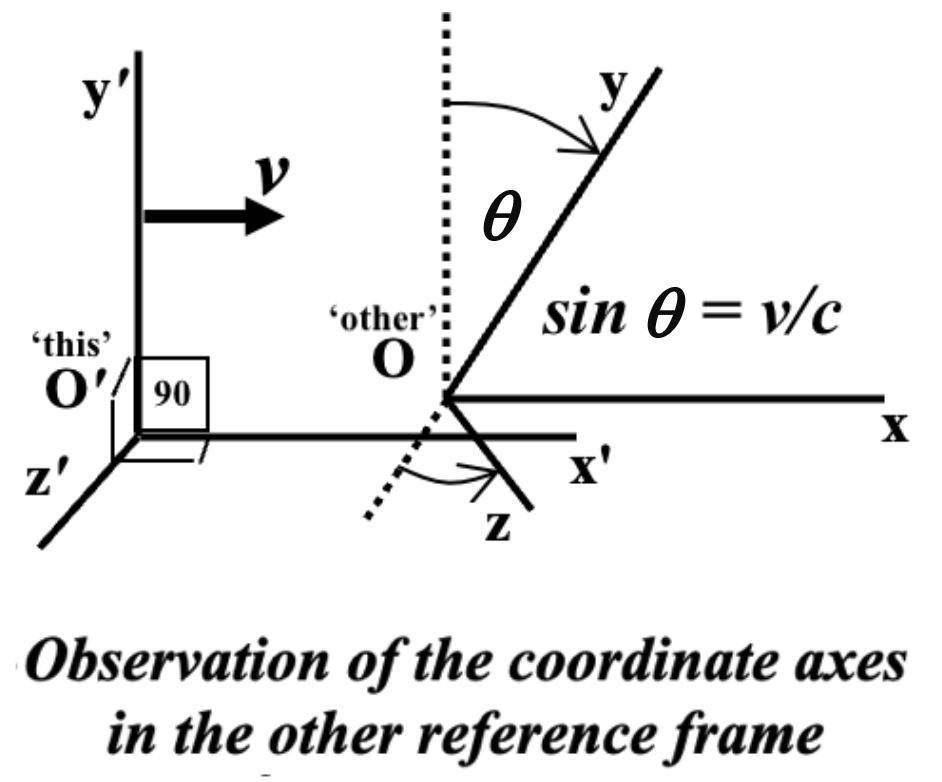
In a similar way to how ‘infinitesimal path difference’, Delta-d has traditionally been defined as the distance between two nearby points along a curve in 3-space such that Delta-d 2 = Delta-x 2 + Delta-y 2 + Delta-z 2, the path difference Delta-S2 (in this case of relativity) defined exclusively as the squared quantity between events is defined for a four-dimensional spacetime continuum. It can be elaborated using four component quantities that reflect the extent of difference in the four associated coordinate values to obtain:
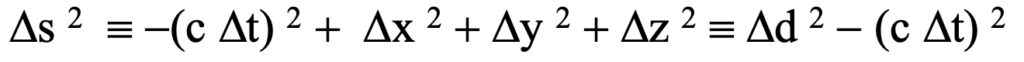
Here you will note the convention whereby the square of the temporal difference in the occurrence times of the related events is subtracted from, rather than added to, spatial aspects of event differences. This is a convention – the respective signs are sometimes reversed – but that a difference (rather than a sum) is involved is essential to its meaning.
The spacetime interval is exemplary of how covariance is handled in situations involving relative motion.
Some perspective
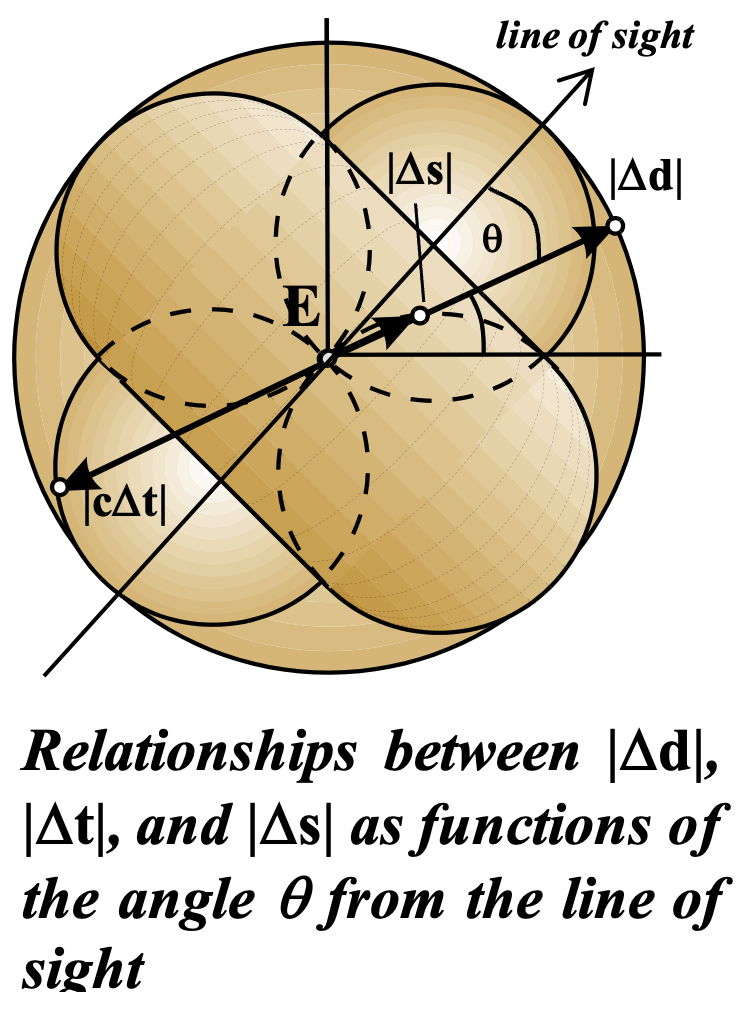
Before moving on, and just for clarification of the rather non-intuitive nature of the spacetime interval, consider that the value of the spacetime interval to every event you observe is zero! A non-trivial spacetime interval is not an ‘observable’ in physics. With regard to distant galaxies, and in particular an event E associated with emission of a single photon of light that occurs in a galaxy a billion years ago (away), one can consider the space time interval between that event and an associated observation event that may occur in a galaxy within a vicinity of E as assessed in our spacetime. Events in other galaxies along our same line of sight will all have spatial components of the spacetime interval canceled by the temporal components. Those at approximately right angles to, and at short distances from, our line of sight to E will have virtually all of the spacetime interval equal to its spatial component.
In short, if two events occur simultaneously for an observer (us in this case), indicating that Delta-t is zero, then the spacetime interval becomes just the spatial separation between the two events. In general if,
the spacetime interval will reflect the spatial difference between the events in the frame of reference of an observer for which the events occur simultaneously. Notice that in this case there can be no possible interaction between the events. And if,
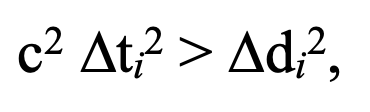
no observer in any frame can possibly witness the two events as occurring simultaneously. If, as the only other alternative,
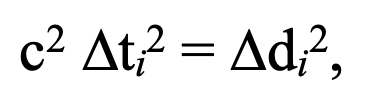
the time difference is the transmission time between the emission and absorption of a photon of electromagnetic radiation.
Relationships between Delta-s2, and Delta-d2 and Delta-t2 are illustrated in the figure above for a unit spherical spatial difference about some remote observed event E. This mapping is of a sphere onto a torus as shown. Clearly, despite its usefulness in certain cases, the spacetime interval is not based on observations and is a quite non-intuitive construct.
Is this accommodated by the observation transformation?
Between the occurrence of an event and its observation (also an event) in relatively moving reference frames, the equation (c Delta-t)2 = Delta-d2 holds. This reflects the universality of the speed of light since this relation holds in every reference frame. This is supported under Lorentz transformation as well as the observation transformation that acknowledges misalignment of the reference frames as mentioned above. Working through this for what we refer to as the ‘observation transformation’, one obtains:
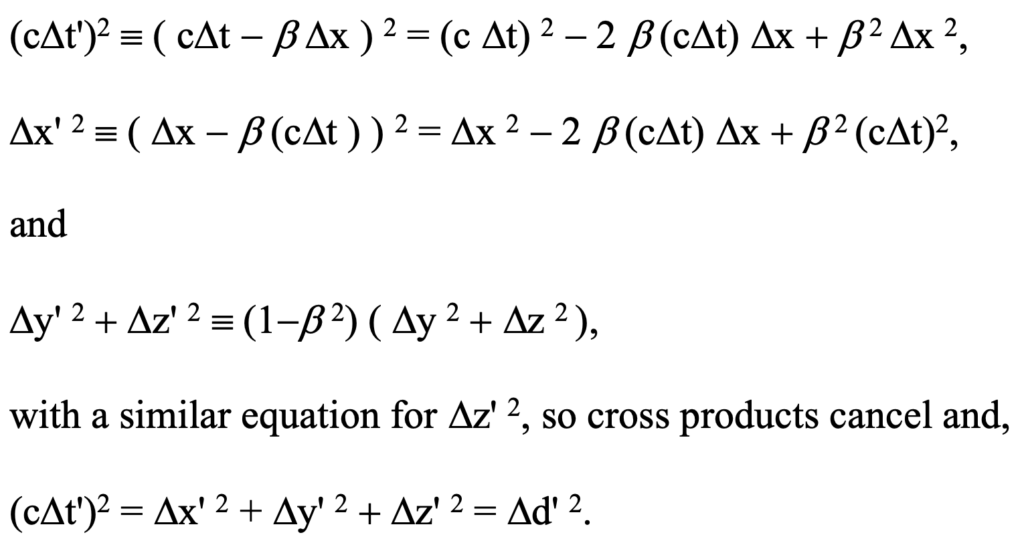
This demonstrates the universality of the speed of light in a vacuum for the observation transformation.
However, this does not hold true when one extends the meaning of Delta-s2 to include differences between events other than those uniting two observers by emission and detection of the same photons. The cancellation of the factor (1-beta 2) in the equations of a photon’s path that guarantees Delta-s2 = 0 as an invariant, does not guarantee invariance in all cases without extending the scheme. What we find is that:
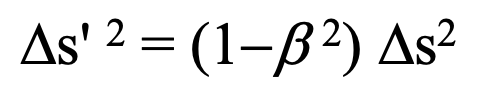
In special relativity this leading factor is cancelled by its inverse (gamma2) in the Delta-x’2 and (c Delta-t’)2 equations and isn’t required in the Delta-y’2 and Delta-z’2 equations. This leading factor is a reality of the observation transformation. So does this mean that observational relativity is thereby invalidated? No. It does, however, necessitate that a different ‘metric’ be used to reflect the observed phenomenological differences in the unique relative geometries for which mutual orthogonality is not realized as mentioned above.
What is a metric?
In rigorous formalities employing Einstein’s tensor notation, the spacetime metric, gm n (analogous to self-metric Im n defined above) is co-defined with the spacetime interval in generalizing relativity, as follows:
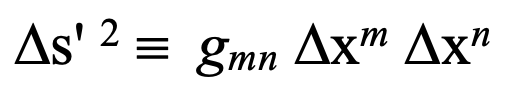
where
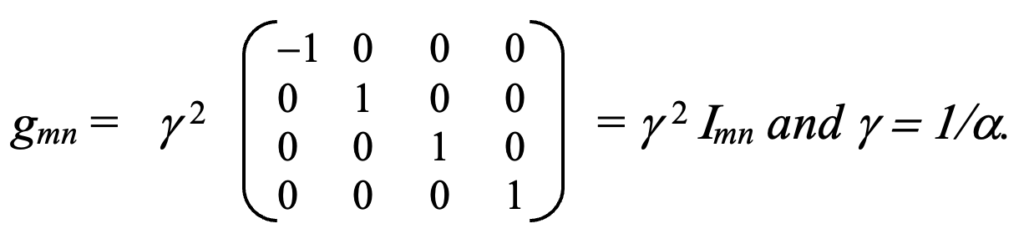
using tensor notation where Delta-x, is a 1-form, not a vector per se.
In the dogma of special relativity, observers in uniform relative motion are assumed to share a common metric Im n , whereas observational relativity absorbs the all too obvious observed geometrical differences into the metric gm n instead. This is very much as it was done much later in generalization process in ‘general relativity’.
Formally this metric is called into play in both theories to express covariant physical laws in tensor notation such as those involving an electromagnetic ‘field strength tensor’ in generalizing electrodynamics. It is used in defining a covariant derivative, and to ‘raise’ and ‘lower’ indices as a part of manipulating tensor constructs between vectors and 1-forms, for example. So insisting on accepting observed aspects of relativity has not forced us to reject either covariance or generalization, but merely to address them more formally at an earlier stage of generalization. In fact this alternative approach embraces them in a more direct and legitimate way by employing a non-trivial metric and its inverse for all relative motion.
Some perspective
The observation transformation addresses the fact that uniformly moving observers do not share geometrical relations among observed events, and therefore (unlike in the special theory which presumes otherwise) any metric presuming to encapsulate this geometrical aspect of relative motion must be unique to that particular relationship. The perspective differences of uniformly moving observers have been more or less trivialized in their 4-space generalization in special relativity by characterizing a mutual spacetime as merely ‘flat’. It isn’t flat. Special relativity presumes that their relative metrics are identical with their self-metrics or identity matrix. This is the reason for introducing observational relativity. It acknowledges that respective coordinate axes are not (and cannot be) aligned despite insistence to the contrary.
The fact that angles to mutually observed events from coincident observers are askew with regard to each other, while perhaps seeming to some (including Roger Penrose and other pre-eminent physicists) as merely a minor embarrassment, is a situation of major significance. This is equally the case from mathematical, physical, and philosophical perspectives. That is what distinguishes ‘observational’ from the ‘special’ theory of relativity. Increasingly relativity theorists have assumed that spacetime provides a platonic underlying reality rather than merely establishing relations that apply to respective observations of physical reality as Kant would have insisted. Lest this acknowledgement of differences be confused with that for which objects are presumed to actually be contracted even though they do not appear to be, consider that here we embrace actualities that are observed by both observers, characterizing the relationship between actualizable observations – not metaphysical realities! With regard to the presumption of some ‘underlying reality’, as Newton said, we “frame no hypothesis.”
The metric as employed in observational relativity characterizes the geometrical relationship associated with the dynamical situation of the two relatively moving observers – hence the term relative metric. Thus, it does not directly say anything about nature or reality, but simply about the relationship between nominal observations. By employing metrics in this way, undeniable observational similarity can be established that justifies some level of philosophical realism with regard to common sources of events observed from relatively unique dynamical perspectives. That geometrical relations imposed upon these observations made from these various perspectives are ineluctably unique, implies that geometry as such is not an aspect of nature so-conceived – the opinions of the most influential scientists of the last and current century notwithstanding. This uniqueness can, of course, be encompassed by metrics that address the relationships induced by the relative motions of any two observers’ geometries so as to recover invariance to their formulation of apparent behavior of phenomena without presupposing an absolute underlying spacetime, nor therefore any ‘spacetime geometry’ as accepted by establishment. So spacetime need not (nor can it accurately) be considered the least common denominator of reality itself. As space was previously conceived by Kant, Russell, and others, this approach addresses the imposition of pure reason in the form of a geometrical understanding of reality upon reality itself more or less as Einstein originally envisioned as a basis for his relativity.
The relative metric supports the covariant formulation of phenominal behavior. A reality that did not accommodate such a capability is virtually inconceivable.
Leave a Reply