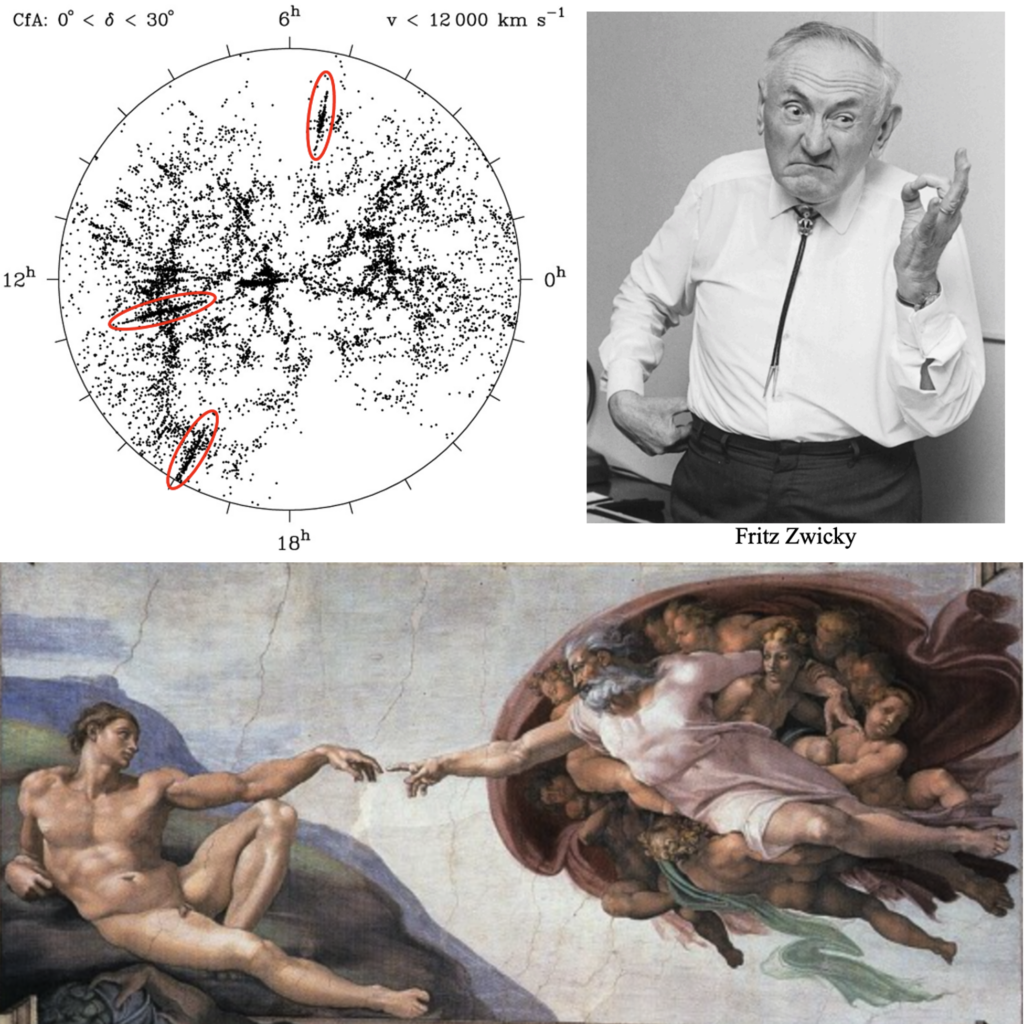
Instead of questioning the immediate phenomena associated with streaks in galaxy surveys that put us at the center of the universe, cosmologists deflect with the humor of Zwicky and enquire into the dark matter that could account for them. One could as well say, “God did it,” and ask, “Why on earth did he do that?” But instead we ask a ridiculous but quasi-scientific question, “Is the invisible substance hot or cold?” But not, “How can it deflect light if it doesn’t interact with light that has no rest mass?” It’s evidently just some aspects of light it can’t deal with.
That’s where we are.
So let’s go back to galaxy survey observations of dark cosmological streaks aligning themselves along our lines of sight. Massive galaxies, mind you, are aligned as though they have a special relationship with us. So, how did such massive galaxies get so aligned? They didn’t! It’s just the metric of the survey with each galaxy placed as a dot at an observed position (d, q ) on the map, where q is an angle and d a radial distance on the map. ‘Map!’ The d isn’t distance, and more significantly, it isn’t velocity either. It is a unitless spectroscopic parameter that is redshift dispersion. Including a unit with it reduces a straightforward fact to a mere conjecture. To associate redshift exclusively with velocity is to suppose that these galaxies are moving at rates sufficient to tear a cluster apart, so extra mass is the deus ex machina. An orbital velocity that is greater by a factor of the square root of two than what is implied by the baryonic mass converts a viable orbit into an escape trajectory. If the assumptions were true dark matter saves the day.
That is not to say such analyses are incorrect; the virial theorem is called a theorem because it is proven. Assumptions aren’t – they are what we assume to be true. Where is it written that all redshift is caused by Doppler? What if only the portion of the observed redshift dispersion that is virial in nature is determined by observed (i.e., not invisible) baryonic matter, and the rest is due to something else entirely?
That is the proposition.
Altogether, galaxies are a small fraction of the total baryonic mass of the more extended cluster cells. The reason galaxies are clustered together near the center of these cells is that the cells are in ‘hydrostatic equilibrium,’ in which outward thermodynamic pressure and inward gravitational force are nearly equal, so the amount of kinetic energy attributable must also be about equal.
Hydrostatic equilibrium is just the statement that a pressure gradient can withstand a gravitating fluid:
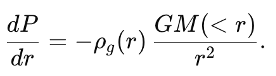
This merely says, ifthe intracluster gas is not rapidly exploding outward or collapsing inward, then the inward gravitational pull is balanced (on average) by the outward pressure gradient. And this the part that matters: There is ‘degeneracy’ (i.e., six of one and half a dozen of the other) with regard to explaining those observed Fingers-of-God (FoG). They are line-of-sight stretchingof cluster galaxy locations when plotted in redshift space. In the orthodox story that stretching is attributed to the Doppler effect of galaxies moving at high speed in a deep potential well. That effect would cause their redshifts to scatter symmetrically both in front of and behind the cluster’s comoving (if indeed there is expansion) center.
But hydrostatic equilibrium says something deeper than “a clusters is stable.” It says that “the same gravitational field that produces large virial velocities also produces a large amount of gas pressure,” because that is what balances gravity. And pressure is not an abstract word here. In a plasma it is literally the product of density and temperature:
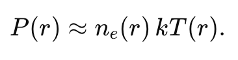
A cluster with a high inferred velocity dispersion (i.e., FoG) has—via hydrostatic equilibrium—a plasma configuration with high pressure in the same region.
That is the degeneracy.
Virial implications derive from a deep gravitational potential, which produces large characteristic velocities, which in turn results in large Doppler scatter in redshift.
The existence of highly ionized plasma also derives from the deep potential that produces the counter forces giving rise to high temperature and pressure gradients. This accommodates large line-of-sight plasma ‘column effects’ of whatever microphysical mechanisms might affect light transmission.
The non-kinematic plasma redshift contribution effects would scale like the virial effects. The same mass field. Same spatial structure. Two different ‘channels’ that can produce the same kind of redshift–space stretching. This is why a redshift correlation function alone can’t tell you what is responsible for the FoGs. Because cluster dynamics don’t bifurcate to give you either a virial velocity or pressure independently. It gives you a gravitational potential and thermodynamic response that simultaneously determine both the virial velocity scale and the plasma gas pressure profile, both required to keep the cell from collapsing. This FoG redshift dispersion can be expressed as:
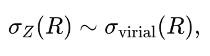
then hydrostatic equilibrium makes it plausible to write a competing contribution of the form,
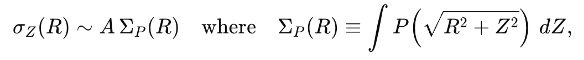
or (depending on the mechanism) an integral over ne, or neT, or ne f(T). The exact kernel can be argued later. The point right now is that whatever the functionality of the plasma kernel turns out to be, it will inevitably be spatially organized the same as what organizes the galaxies. Of course clusters have a spatial distribution that affects their redshift correlation functionality. But if one attributes all FoG dispersion to the Doppler, effect you’re implicitly assuming the plasma actively participating in the same potential well has no line-of-sight redshift influence worth a mention — even though it is the dominant baryonic massive component of the cell and carries enormous thermal energy density.
Where is the necessity of the Doppler assumption written down? And why should it be taken as sacrosanct?
However uncomfortable it may be, “cluster zero” is not a God-given comoving coordinate. It’s a convention—often tied to the brightest central galaxy (BCG) or the mean redshift of members. A symmetric velocity dispersion naturally centers itself around that convention. A plasma column effect does not have to. Once you define the mean redshift away, what survives is not that “front galaxies may show up behind cluster zero and back galaxies in front since as they will be spread in velocity space, but the stretching that occurs along lines of sight through the cluster whether there happens to be a galaxy there or not.
That’s where the degeneracy hides: both mechanisms produce a radially dependent stretching that mimics a power-law over a couple decades in scale. So if plasma contributes even some modest fraction of the line-of-sight redshift dispersion, the standard inference that the length of the FoG is determined by galaxy velocity, which derives from cluster mass, is no longer unique. It seems much more likely to be a combination of both, reducing the requirement for unknown, invisible matter to push the galaxies faster than baryonic matter can support.
And that’s the wedge: not a denial of virial motion (the theorem stands), but a challenge to the exclusive interpretation of redshift-space distortions.
That is the proposition.
Leave a Reply