
To begin, assume that at every point in space there is a probabilistic presence of a secondary radiator (an electron) that, were it present, would oscillate in resonance when an electromagnetic wave front passes. Its resonant oscillations would transmit secondary radiation, at the frequency of the passing wavefront. In Huygens’ concept as elaborated more fully by Kirchoff, and then Oseen, Born, and Wolf, whatever secondary radiators exist at these points in space, they were considered to be stationary with respect to the source of the incident ‘primary’ radiation. Wolf (1986) demonstrated proof of a ‘scaling law’ stating that the scattering of radiation through the intermediate secondary radiators does not alter the spectrum of the original radiation.
Relativity modifies that picture somewhat. If the original source of the primary radiation is moving with respect to the current secondary source at the point in space being considered, if there are no earlier intermediate secondary radiators, then one at this location would oscillate at an increased or decreased frequency associated with the relative motion of source and secondary radiator. That frequency will then be carried forward to the next secondary radiator, etc. So, if there were no secondary radiators or all secondary radiators were stationary with regard to either the original source or ultimate observer, they would have no net effect on the frequency that will be due to relative motion of source and observer. This would also be the case if the secondary radiators exhibited a ‘comoving’ velocity gradually mediating the velocity difference between the ultimate source and observer.
High temperature primary sources of radiation
Observed sources of radiation involve many individual emissions of radiation, each of which is affected by its motion relative to the centroid of the radiation source. That relative motion has the effect of changing its frequency so there will be a line broadening whose width is determined by the temperature of the source. This broadening will by and large be symmetric about the characteristic frequency of the emission. I said ‘by-and large’ because there is also transverse Doppler that involves the second power of the component of velocity perpendicular to the line of sight to the emission. The square of the velocity assures that its effect is always to slightly decrease frequency.
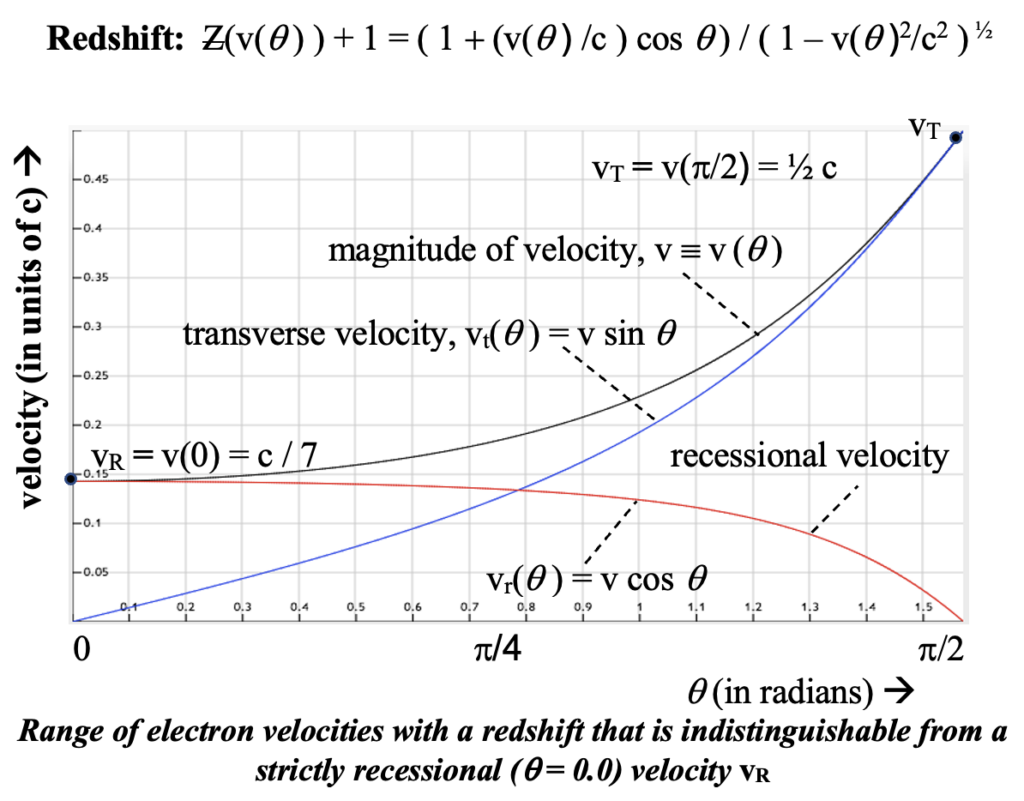
Such broadening will be unaffected by cold (relatively inactive) intermediate secondary radiators or comoving radiators.
High temperature secondary sources of radiation
Wolf’s proof of the scaling law demonstrating the invariance of spectra by secondary radiators did not take relativistic effects into account. That omission invalidates his proof in the context of intergalactic plasma. Wolf was able to show that the law could be violated in a single scattering situation by violating these conditions. That was all. But one must consider the possibility that temperatures and its implied effect on secondary radiator velocities might affect the spectrum of the secondary radiation and any accumulating effect of on-going forward scattering.
The first order radial velocities of media electrons would alter the frequency of the secondary radiation proceeding forwarded through scattering. If one assumes a constant temperature of the medium throughout a transmission region, then the red and blue shifts produced by individual secondary radiators would cancel to at least fourth order in velocity after many encounters with an ongoing wave function. So it would look like the temperature of the medium would indeed make no difference.
But there is a transverse effect of secondary radiator velocities that must be taken into account. That effect is profound. We will be discussing that.
Leave a Reply