I think it is fair to say that if Donald Trump were ever to become aware of, and then bestow his brilliance on, the subject of entropy, he would simply say, “Who ever knew it could be so complicated.” Well, as with other topics that have boggled his mind from time to time, everyone knew. Some of the greatest minds over the last several centuries have struggled to figure it out without success. So, yes, it’s complicated but most of those who tried and failed are safely dead so he can’t fire them.
The significant portion of this post is taken from chapter 13 of the book that is available on this site. Here. The chapter began with the quote from Prigogine and Stengers book, Order Out Of Chaos, (pp. 241-243)
“Boltzmann … wanted to describe not only the state of equilibrium but also evolution toward the Maxwellian distribution. He wanted to discover the molecular mechanism that corresponds to the increase of entropy, the mechanism that drives a system from an arbitrary distribution of velocities toward equilibrium.”
“…Can we conclude that the problem of irreversibility has been solved, that Boltzmann’s theory has reduced entropy to dynamics? No, it has not..”
It is clear that Boltzmann devised this ‘H theorem’ to prove the irreversible succession of submicroscopic states to a stable equilibrium. It was the culmination of his effort to achieve a reductionist explanation of entropy. The theorem is not even required in a milder form of Boltzmann’s derivation of the Maxwell-Boltzmann distribution.
Boltzmann’s Notable Failure To Find The Origin of Irreversibility
Realization of the stable Maxwell-Boltzmann distribution (shown below) is merely sufficient but not a necessary condition for equilibrium; various anomalous conditions can also result in stability as demonstrated by Prigogine and Stengers. But irreversibility makes no entry whatsoever in the reduction of thermodynamics to the kinetic theory by Boltzmann’s analyses; it had slipped through fingers again.
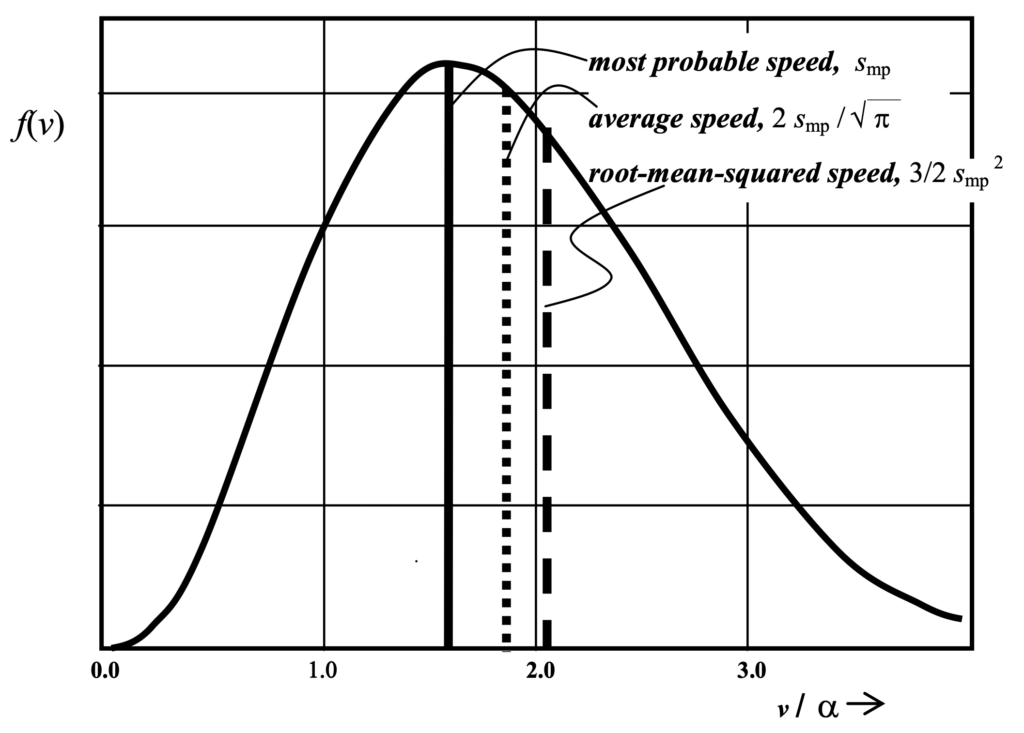
Maxwell-Boltzmann velocity distribution
What the H Theorem does imply is that, although there might possibly be some other (even if previously unknown) distribution that pertains in some situations of equilibrium, certainly the realization of Maxwell’s distribution does indeed imply equilibrium in any case. This statement is easily proven by Boltzmann’s analysis but the reverse is not. So does the H theorem imply that there is indeed a necessary trend of microstates into only those for which the exponential distribution function applies? No.
The less stringent, but still extremely powerful, constraint is worth some thought. Furthermore, there are well known phenomena such as chemical clocks for which the more stringent necessity condition obviously does not apply. In such cases a form of reversibility would seem to be realized to within the accuracy of Boltzmann’s analyses even at the macroscopic level of our everyday existence. The sufficiency condition simply implies that whether velocities are reversed, which in most conceptions is tantamount to time reversibility, or not, the system will indeed proceed to a ‘stationary state’ characterized by conditions that typically do, but need not in all cases imply the Maxwell- Boltzmann distribution of energies.
Another aspect of thermodynamic irreversibility is that involving the gradual dissipation of energy from (or to) a local system into (or out of) a larger global system or the entire universe. Here the local system may remain always in an instantaneous quasi equilibrium, but will nonetheless suffer irreversible losses of energy over time until and unless it is in a totally isolated static equilibrium with its global environment. Certainly these two aspects of irreversibility may produce similar phenomena and involve much commonality in explanation, but they pertain to quite differently described physical situations.
the association of ‘H’ with entropy
We noted earlier Boltzmann’s definition of the parameter H as a part of what he called his H Theorem in his rigorous derivation of the Maxwell-Boltzmann distribution of molecular velocities based on the conservation laws applicable to molecular collisions. Boltzmann defined, H as the Integral from zero to infinity of the velocity distribution function, f (v) times the natural logarithm of that distribution, ln ( f (v) )
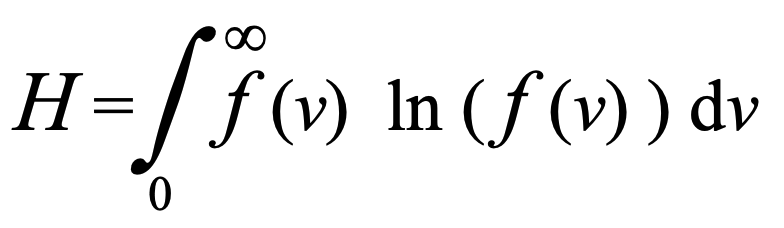
Here v is the magnitude of the velocity (speed) of molecules within a gas and f (v) is the distribution of those speeds throughout the gas. As discussed previously, he showed that,
dH/dt < 0.
This conclusion is reminiscent of claims for entropy, S, except that entropy was conventionally defined in a negative sense such that,
dS/dt >= 0.
So it was quite natural to wonder whether H might be a submicroscopic classical mechanical descriptor of entropy itself. In which case, a reduction of the macroscopic state property, entropy, would have been achieved as anticipated earlier in determining effects of rapid change in pressure on the energetics of the molecular constituents of a gas.
It can be shown by rigorous analyses based on Boltzmann’s work, but getting into the discipline of statistical mechanics which is beyond the scope of this post, that for a monatomic gas in equilibrium, the following relationship does indeed hold:
S = – k H
Heuristic arguments to provide confidence in this conclusion.
Thus, it is possible to reduce the description of entropy to the submicroscopic level by a completely mechanically-based expression for entropy. And although Boltzmann’s achievements were indeed significant, including much of what we currently know about thermodynamics — heat and entropy in particular — he could not adequately explain the inevitability of increases in entropy in approaching equilibrium since the reversible conservation laws from which equilibrium derives do not preclude reversal of that progress. So although on the one hand, his association of H with entropy was persuasive, nonetheless his H theorem could not be applied to convincingly prove the inevitability that is the hallmark of entropy.
the criticisms of Boltzmann’s conclusion
Boltzmann later had to conclude, that even this proof could not account for irreversible changes in mechanical systems. His theorem had captured the nature of entropy as a description even though certainly not as an explanation of its origin.
If one were to reverse velocities of all particles (what had been considered tantamount to reversibility) at any point in time in accordance with Lochschmidt’s criticism of Boltzmann’s precipitous claim of explanation, the theorem would still apply. Entropy would as surely increase into the past and not uniquely into the future as the arrow of time indicates it must. Increasing entropy would not have been exclusively associated with irreversible behavior. Thus, the long sought explanation was ultimately to elude Boltzmann. His effort certainly had resulted in a brilliant derivation of Maxwell’s equilibrium velocity distribution of the constituent molecules. But the result totally obscured any rationale with regard to distinguishing the issues of reversibility and irreversibility.
The plausibility of the precise balance he had thought he had proven must be considered. One cannot, of course, imagine a counter process of the collisions he analyzed whereby an equilibrium so achieved would be frittered away, although that would seem to be a reasonable reticence from Lochschmidt’s critique. There is something that Boltzmann and his critics alike had overlooked. Both the analysis of the dynamical processes and the critique seem intuitively valid although there was at the time no discernible flaw in either. The flaw of course is the omission of the significant role radiation plays in the mediation of the exchanges between molecules that is outside the scope of the model implemented by Boltzmann.
So although on the one hand Boltzmann did discover a tremendous amount of useful information concerning behavior of submicroscopic constituents of gases in equilibrium, he most certainly did not discover the origin of irreversibility with which he had become obsessed.
the significance of Boltzmann’s work
Let us consider Boltzmann’s own impression of the significance of his ‘H Theorem’ in this regard. He realized that his model involved completely reversible processes and yet felt convinced that he could demonstrate how these completely reversible mechanical operations were ultimately responsible for the origin of the notably irreversible behavior of the second law of thermodynamics. Certainly it was not implicit in Boltzmann’s understanding of phenomena at this level of analysis that a molecule becomes ‘hot’ by the impact of another molecule and thereby radiates thermal energy that would not otherwise be emitted as a merely unrelated normal atomic emission. But something similar to that must have seemed to him like what must happen in actuality. The concept of heat must always have been entwined with the colors given off in thermal radiation and yet that aspect of what heat ‘is’ never seems to have been exploited. There are other, more clearly relevant, aspects of heat than just molecules in motion. We will address this specifically in another post.
Boltzmann believed that he had found the source of irreversibility in his ‘necessary and sufficient’ condition. His efforts with regard to the concept of irreversibility exhibit a couple of most interesting facets. One is that associated with Boltzmann’s ‘H theorem’ whereby a system of particles that continues to satisfy the reversible conservation laws tends irreversibly toward an equilibrium characterized by the Maxwell- Boltzmann distribution of energies. Since persistence of the conservation laws was assumed throughout Boltzmann’s derivation, there was assumed to be no dissipation (whether by radiation or anything else) of total the energy of the system. So the extreme initial optimism is hard to comprehend.
He defined the quantity H as the integral (or the summation in discrete finite element systems) of the composite distribution function f(v) times the logarithm of f(v) where integration (or summation) is over all possible velocities. In deriving the function f(v) representing the distribution of energy apportioned to individual particles of the system, he dmonstrated that it must be an exponential function when the system is in equilibrium:
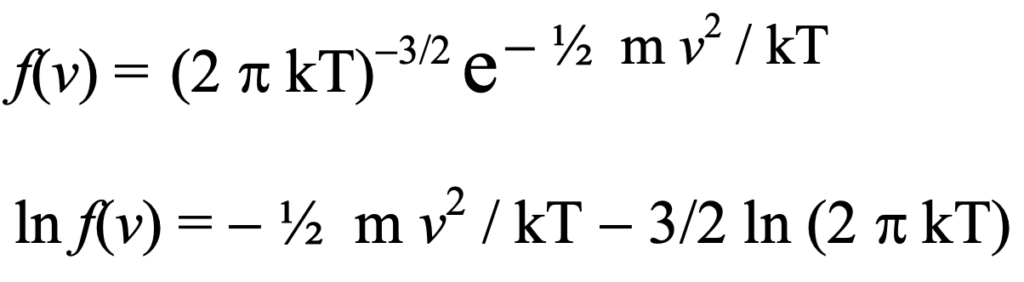
So naturally, the integral over all possible velocities of the Maxwell- Boltzmann distribution times the log of that distribution is always negative except at absolute zero where the molecular velocities would be zero. This is a proof of Boltzmann’s H Theorem, not a proof that the H theorem has any especial significance.
Leave a Reply