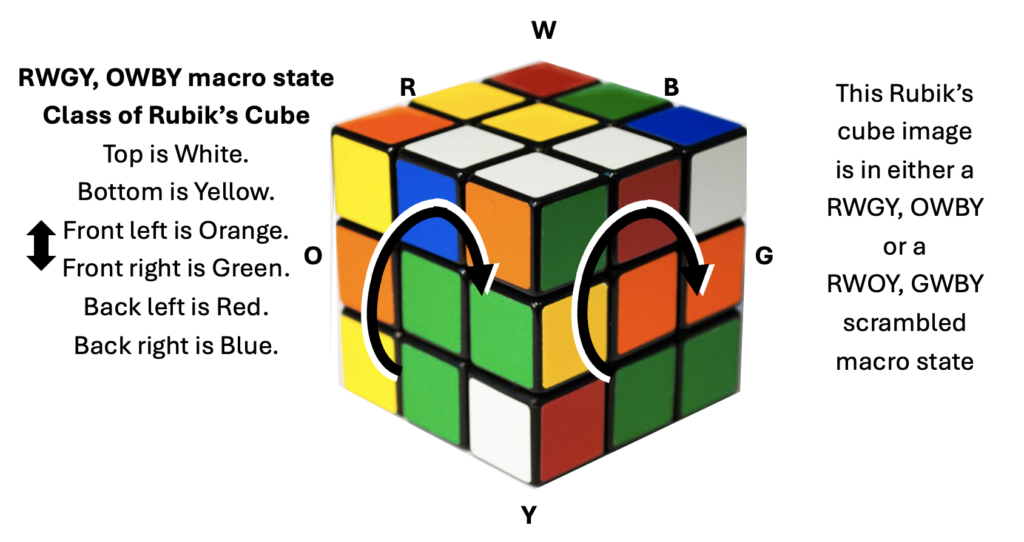
It can be shown that there are 43,252,003,274,489,856,000 possible permutations, i.e., ‘states’, of the 3×3 Rubik’s Cube. This is a huge space of possibilities, but there are approaches to meandering through this phase space without getting lost. In the following figure, one can infer the relative positions of the colored faces from the image of its current state. Proceeding from the back left, top, front right, to bottom we have either red, white, green, yellow (RWGY) or RWOY, leaving either OWBY or GWBY, respectively.
Some years ago a mathematician received a Fields Medal award for showing that even in huge phase spaces there are subspaces defined by group operations that allow one to perambulate on a closed path through the space by repeating cyclic combinations that get one back to an original state. So if a Rubik’s Cube is in a legitimate scramble of a solved state, one can get back to that solved state by the repetition of the sequence of rotating the right side of the cube clockwise through 90 degrees followed by rotating the front side clockwise through 90 degrees. This will, after some number of repetitions, but involving relatively few states, return the cube back to its solved state. Other prescribed sequences will define other closed paths through different states that return the cube back to its initial state.
If one begins twisting a Rubik’s Cube at random, one can pass through a huge number of different and confusingly unresolved states without returning to the solution. There are 5 factorial (120) ways the six colors could have been assigned to faces of the cube by the manufacturer or someone messing with the decals. Whether it is possible to change the relative position of a decal to render the puzzle unsolvable, I leave as an exercise. The Rubik’s Cube is usually configured as RWOY, GWBY when it is sold. I don’t know why. All of that vast number of permutations correspond to one of the 120 choices made by the manufacturer or the devious daughter who removes the stickers and replaces them to befuddle her brother. But the solved state exists in a smaller group of states defined by the regimen used in solving the puzzle.
Leave a Reply