Errata

I don’t need to tell you that I make mistakes.  I suppose it’s a matter of salvaging self-esteem that I engage in this.  Be that as it may, I don’t like being as error prone as I am.  But whenever I look at one of the books I have written, I am amazed at how many typographical and grammatical errors I find.  I pride myself in being better than that, but alas I’m not.

Einstein made a big deal about what he considered his “ most egregious” error and indeed, it was a doozie.  His reputation alone has propped it up, warranting repudiations like, “Oh, no sir.  Your lambda is a most useful construct.”  No, it isn’t.  It was an error.  An egregious one.  I was once at a conference where an author argued that it was not a mistake – that it was a godsend for the dark matter world.  I approached him afterward to ask whether it was his considered opinion that Poisson had made a mistake instead.  He laughed at the predicament I had put him in and said, “Yes, I guess I would have to say that, wouldn’t I?”  But, unlike me, Einstein didn’t make many mistakes like that.  Nor certainly did Poisson.

My senior year in physics, Professor Fred Schmidt taught the course on modern physics.  Before handing out the first exam of the quarter, he informed us that we would no longer be given full credit for solving problems correctly if we got the wrong answer.  (That leniency was one of the reasons I preferred physics to engineering.)  Professor Schmidt elaborated that Lord Rayliegh made a mistake in his calculations that Sir James Jeans corrected in reviewing Rayleigh’s proof.  And so it became known as the Rayleigh-Jeans law.  “So you have to learn that mistakes have consequences.”  Anyway, to make a long story short, when he handed out our corrected exams, I had a hand-written 100% on mine.  I had eclipsed my friend George, who sat next to me.  As the professor went over the solutions on the board during that class period, George pointed out that I had made two complimentary arithmetic mistakes that had given me the right answer.  He had not been so fortunate on his single mistake.  “Aren’t you going to tell him,” George asked.  “No, of course not,” I said.  “He should have known that mistakes have consequences.”

Back in the late sixties and early seventies IBM had to reissue OS360, the operating system for their mainframe computer, many times because of errors.  But each time they ‘fixed’ it, it required more fixes than the previous time.  Fixing errors is not a convergent process.  For some time I was the unlikely editor of the journal ‘Gift of Fire’ for which I received submissions of articles from members.  The submissions of one member in particular were invariably rife with his inaccuracies and grammatical errors.  I would point out the errors to him by email and he would resubmit the article too quickly, and always with the comment, “Now it is perfect.”  It wasn’t perfect; it never was – usually we had to interact several times to get it minimally acceptable. So… we flutter around with this fake humility of sorrow for the wrongs we have done as totally out of character.  We assure ourselves that we are so much better than that.  But we’re not.  A friend of mine once gave me the advice that his father, who had supposedly published over a hundred books, had given him:  “Brian,” he told his cautious son who kept going over his only book, “you can spend ten years getting out every error in your book or you can write ten books.” 

I guess I lean toward the latter.

The other day I noticed that the first line of the fourth paragraph of my latest novel reads:  “The coffee pot had filled after having been set *** it *** in motion a while ago.”  Not good!  And it’s on sale.  But more egregiously, my scientific works have inexcusable errors that inflict serious damage on the credibility of what I consider Nobel quality stuff.  (That’s a feeble attempt at humor by the way, not a mistake.)

My model of cosmological redshift is a case in point where I put together a chart of which I have been very proud.  But it contains serious errors. Those errors are in the derivation of unique relationships applying to extremely short wavelength radiation.  It is not unique.  It’s the same curve, but because of longer extinction intervals for shorter wavelengths, the step sizes are larger.

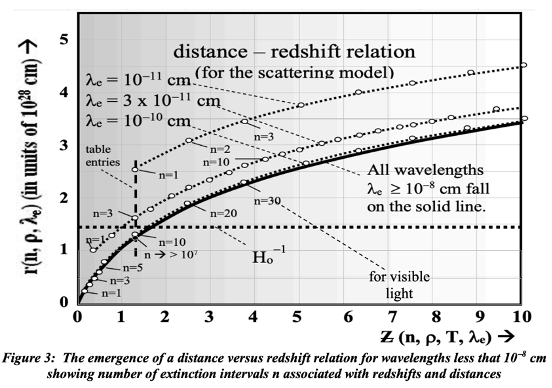
I’m truly sorry I cannot list all my errors of consequence; it would be impossible.  I will not dedicate the ten years required to correct even a portion of all the errors. I think my ideas are sound and I hope readers will put out the effort to realize that most errors of expression do not invalidate ideas.