Follow up on critique by ChatGPT PRO 5 on cosmology papers on this site

In my last post I provided ChatGPT’s complete review of all the technical cosmology and physics-related papers on this site. I provided rebuttals where I thought they were appropriate and have since asked ChatGPT to inform me of which of my rebuttals it considered insufficient. I’m working through them. But here is one that might need some clarification.

ChatGPT concern:

My rebuttal:

Not satisfied with my response, ChatGPT insisted that I owed my readers a more detailed explanation. So here it is and it is largely taken from pages 491 to 496 of my 2009 book, Cosmological Effects of Scattering in the Intergalactic Medium.

Is the hydrogen-helium ratio a coincidence?

…

The amount of energy distributed throughout our universe as background radiation is extremely closely matched to the amount of energy released by the production of the known percentage of helium and traces of other elements from a primordial hydrogenous plasma.  There is no required violation of the conservation of energy or other time-honored laws of physics in supposing that the energy given off in producing that observable fact must still exist in some form or other in our universe today.  Where else could it have gone?  These are two extremely significant universal numbers – the relative abundance of the first two elements and the energy density of background radiation.  It would constitute a dereliction of scientific duty to ignore the obvious relationship between these two facts.  This is especially the case when the two pertinent energy values happen to be in such complete agreement.

…

The current evidence overwhelmingly suggests that these two contemporaneously relevant numbers are intimately related.  Occam’s razor must certainly demand the simplest solution that relates the energy released as radiation in creating helium and the observed energy in the microwave background radiation.  This obvious connection would have to be totally disregarded to accept the extravagant Rube Goldberg mechanism employed by the standard cosmological model instead.

A directly measurable amount of energy went into the universe with conversion of 24% (by mass) of primordial hydrogen into helium, and there is also an observable resulting radiational energy output.  These two energy densities match precisely at the current time with no ad hoc assumptions having to be made.  They can be envisioned as a perfectly balanced process.  To ignore that obvious possibility, or to accept an alternative solution for which this coincidence is lost in the ineffectual expenditure of many orders of magnitude more energy than contained in all the matter in our universe to account for a simple fact would be fool hardy.

In Wagoner, Fowler, and Hoyle (1967, pp. 23-24) we find the following, part of which we quoted earlier:

This is quoted here as contributing to the conjecture that the current — and the author tends to believe stationary — kinetic energy state of the universe can account not only for the distribution of the observed background blackbody radiation, but for its perpetuation as well. [This is demonstrated in several papers on this site.]  … This alternative conjecture in the quotation above, i. e., that energy release and “thermalization of energy from recent hydrogen to helium conversion in stars” (emphasis added) is [completely compatible with the plasma scattering model].

…

determining the extent of the agreement

Let us follow up on more accurate current estimates of those quantities identified by Wagoner et al. (1967) in the passage quoted above as they apply to the scattering model predictions.  Their comments pertained to the then-current estimates of mass density and elemental abundance percentages.  Whatever the actual values happen to be, the scattering model must be compatible with them applying at all times in the past and foreseeable future.

In the next chapter we will address the specific thermonuclear reactions that are involved in this fusion sequence from hydrogen to the stable isotope of helium.  There we will find that the difference in the rest mass energy of the nucleons required to produce one helium-4 nucleus minus the rest mass energy of the helium-4 isotope is:

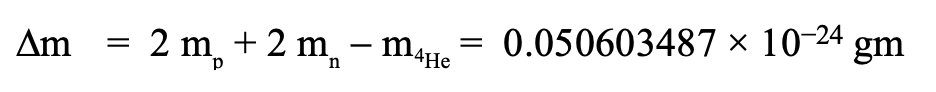
Subscripts p, n, and ⁴He apply respectively to proton, neutron, and alpha particle (⁴He nucleus).  Amounts apply to single nuclei.  The total energy released in creating one gram of helium-4 is therefore:

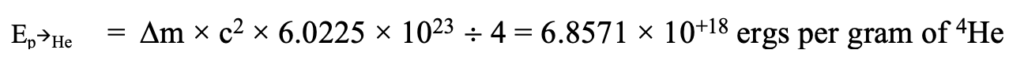
Notice that one mole of any substance involves Avogadro’s number (i. e., 6.0225 × 10²³) constituent molecules — atomic nuclei in this case — with a total mass equal to the atomic number of the substance measured in grams.  For helium with an atomic weight of four, this involves four grams of the substance.  So to assess the energy loss per gram, this has had to be divided by the atomic weight of helium-4.

But to determine the energy density, rho_p->He, which is the amount of this energy per cubic centimeter, we must multiply the result above times the observed universal mass density of helium rho_He (measured in units of grams per cubic centimeter) as follows:

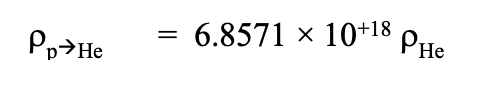
Now for comparison with the quoted Wagoner et al. (1967) comment, notice that the energy per cubic centimeter in the microwave background radiation is slightly less than was estimated when that passage was written over forty years ago.  It is now known that the radiation temperature is 2.725 K rather than 3.0 K.

When this ratio is raised to the fourth power as is appropriate in application of Stefan’s law, it changes the estimate by a factor of:

(2.725 / 3.0)⁴ = 0.6807

This reduces the Wagoner et al. rough estimate of the density of energy in the microwave background, rho_{u bb} to 4.08 x 10^-13 ergs per cm³ from the 6 x 10^-13 ergs per cm³ they estimated in what we quoted above.  We now know that, in fact, it is precisely:

Their estimate was amazingly accurate.