Back before Wile put an end to such misery, amateurs such as I sought a proof of Fermat’s last theorem that, although not fitting in a margin of his book, wouldn’t require 300 pages of heavy-duty math. Okay, I admit to having naively wasted way too much time on it. But even in such a doomed effort, one learns something. One becomes aware of the vast scope of the irrational numbers. This fact was most ably captured by the great mathematician Cantor who in a letter to Dedekind wrote, “I see it but I don’t believe it. There are as many numbers on the side as in the square.” That is the issue with irrationals – their prodigious proliferation. They are numbers out of control. That is what one comes to grasp in a failing effort to prove Fermat’s last theorem, that can be expressed as:
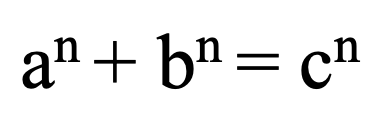
with a, b, c, and n all integers, for which there are no solutions for n greater than 2. This can be ‘simplified’ by writing:
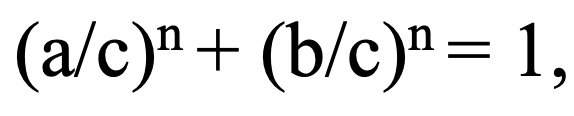
then defining x = a/c and y = b/c, both rational. If one plots y(x) for various integral values of n and
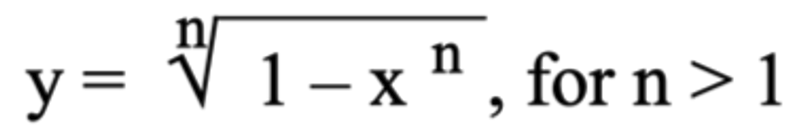
No point on any of those curves for n greater than 2 has a single value of y that is a rational number times any given rational value of x. Yet, one can draw seemingly continuous straight lines at random (a couple have been drawn) for which y is a rational value times a rational x for every x you want to pick along that axis. But of course, those rational pairs do not constitute a continuous line; there are infinitely more points along even those lines (and along the x axis) for which one or both of x and y are irrational.
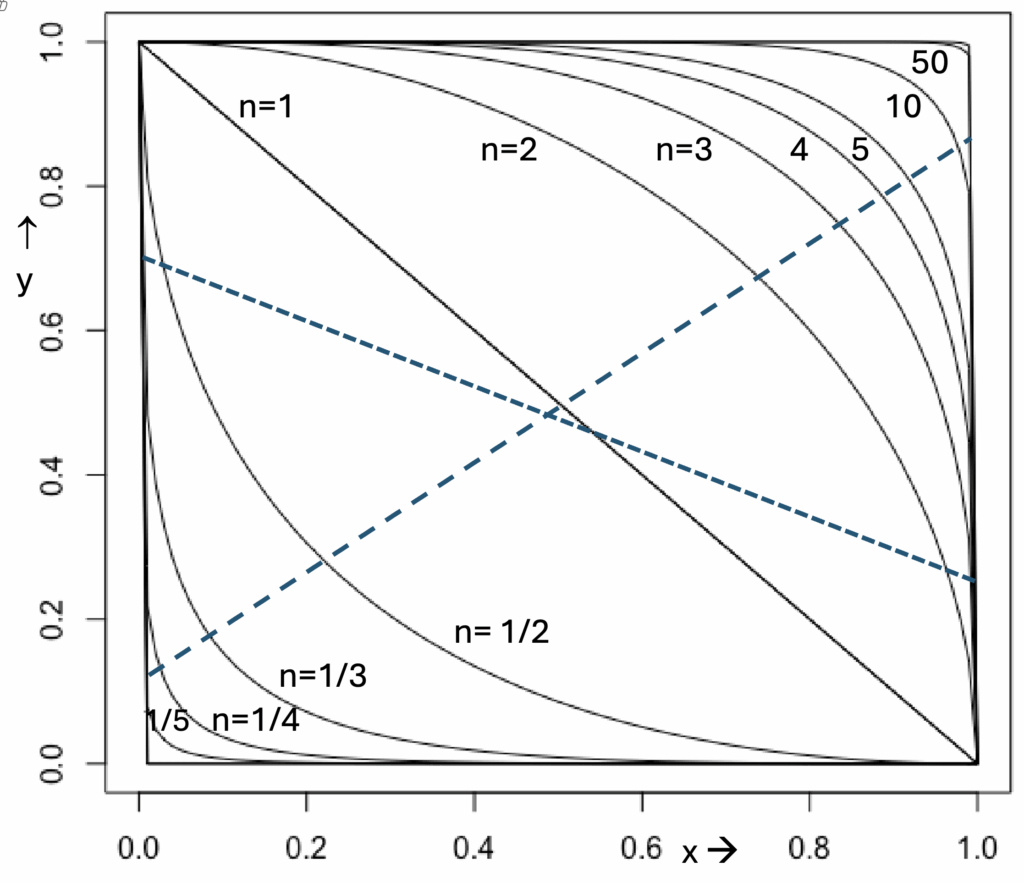
If one were to throw a dart with an infinitesimally sharp point at that unit square, the probability of striking a point representing a pair of rational numerals is virtually zero – smaller than tossing a hundred heads in a row with a fair coin. Or a thousand coins. But there is no point (a zero probability of a point) along any continuous curve for n greater than two that represents a pair of rational numbers. Not a single point! Like Cantor, I can scarcely believe it. Even yet. Even now.
As Cantor had noted, one could color in that complete square with pairs (x,y), both of whose values were rational numbers. It would look that way to the naked eye and to whatever level of magnification one chooses to use. But each of the tiniest pixels that comprise the color of such a square is surrounded in its immediate vicinity by an infinite seething sea of irrational numbers. Irrationals! All those curves for n greater than two dodge and miss every single point for which y is rationally related to x. Fermat shouldn’t have tried to be so cute.
Virtually everything is irrational!
Leave a Reply