I concluded my previous post with the following comment:
“It is reasonable for you to not take my word for it. I could have just taken a marker and drawn curves that fit the data (much better than any standard model) just to fool you as some kind of alternative perverse joke.”
But even if you supposed I had done that, what would be the most reasonable conclusion for you to make? Wouldn’t it be to check out the curves I had drawn to determine what mathematical form they take. Then, whatever physical mechanism you can discover that is isomorphic with those equations would be the correct physical model of the universe. Doesn’t that make sense? One shouldn’t force the universe to fit into a model, one should fit the model to the universe. Of course that is what standard model apologists are attempting to do, but a mansion with too many lean-to additions is not a mansion.
I concluded my remarks in the previous post with this: “Those were plots based on a mathematical model that was derived from the data using accepted physical theory and data of high temperature intergalactic plasma and its affect on light passing through it.” So those are the words you can put to your new model of the universe. I then promised that in subsequent posts I would present a summary of the derivation of the plasma scattering model and its demonstrable effects. What follows is the first installment of that summary. And even though it is a summary, it must be fairly detailed to leave no gaping holes. So in this introductory post I address only the nature of electromagnetic radiation and and how it is affected by the properties of the medium though which it propagates. This basically includes the derivation and implications of the Lorentz-Lorenz formula as it will be applied to the intergalactic plasma medium.
The text and figures (including specific figure numbers) are taken directly from the volume Cosmological Effects of Scattering in the Intergalactic Medium that is available on this site.
Introduction to electromagnetic radiation
Electromagnetic radiation throughout its broad spectrum is, of course, the product of interactions of electrically charged particles – in general one material entity interacts with another by way of electromagnetic transmissions involving the exchange of energy and momentum between particulate matter and radiation. The form of radiations that are emitted and detected are in all cases described by Maxwell’s equations of electrodynamics, which, despite the many subsequent conceptual reevaluations with quantum and relativity theories, still describe that behavior most effectively and with a precision that is very adequate in most every case. The photonic aspect is treated where applicable as a coherency length, etc.
As electromagnetic radiation propagates to greater and greater distances from a relatively localized source, its behavior can be approximated by that of a plane wave with ever increasing accuracy because limited surfaces on very large spheres are nearly planar. This usual assumption is justified to extremely high precision for radiation that propagates to a distance that is considerably greater than the average ‘extinction distance’. This is the minimum distance that radiation must propagate through a medium after which the properties of the medium determine propagation characteristics including its speed. The concept of ‘extinction’ is integral to the concepts of ‘forward scattering’ that we will discuss in detail in the next post. and will be explained in that context in considerably more detail in that post.
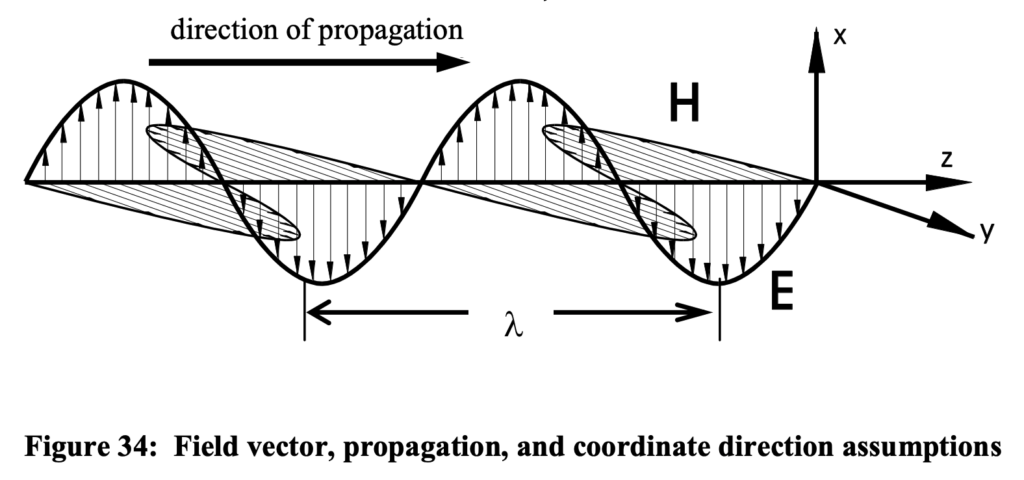
The propagation of the simplified waveforms of electromagnetic radiation along the direction of an arbitrarily chosen positive z axis may be specified using the following expressions:

where the field vectors E(z,t) and H(z,t) are assumed to be polarized such that the electric field E is aligned always with the x axis, whose unit vector is ‘i‘ and the magnetic field H always along the y axis, whose unit vector is ‘j‘. The angular frequency of the radiation is given by omega (w), its wavelength by lambda (l). The index of refraction n possesses a ‘real’ value of unity for propagation through a vacuum implying that there is no ‘imaginary’ part to contribute to absorption; its definition and functional dependence on properties of the medium will be discussed further on. The large ‘e’ symbol is the base of the natural logarithms; it is a number, e = 2.718… , and of course i is the ‘imaginary’ square root of minus one. The scalar quantities E_o and H_o are assumed to be constant over considerable ranges of space and time. Angular frequency and wavelength are related by the formula:

The implied coordinate directions and perspectives employed in analyses to be performed and the figures used to illustrate concepts described throughout this volume are as illustrated in figure 34 below.
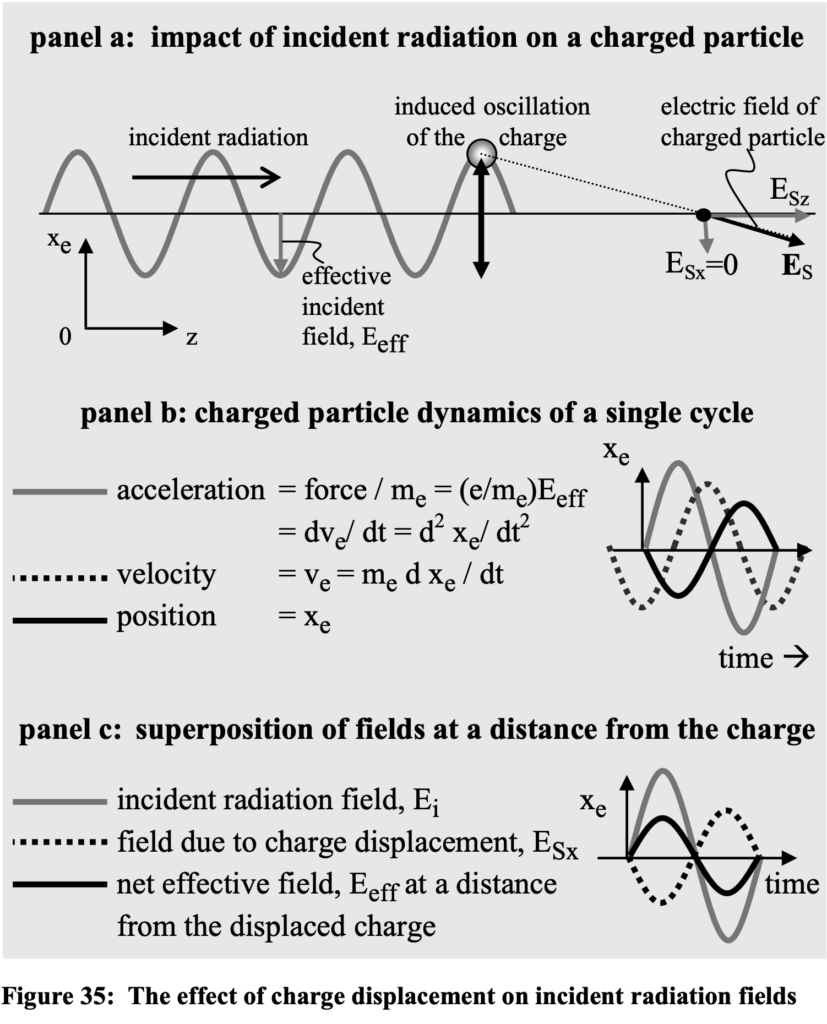
scattering forces imposed on individual material charges
The effect of electromagnetic radiation on material substances is to force the acceleration of individual constituent charges of which the substance is comprised. The same basic phenomena occur whether the constituent charges are more or less loosely bound within atoms, molecules, crystalline structures, or are ‘free’ as in diffuse ionic plasma. The accelerations of charges in a scattering medium can result in absorption of the incident radiation as well as emanations of ‘secondary’ radiation of the same frequency originating at the individual constituent charge. The latter is associated with what is known as ‘forward scattering’. This phenomenon is illustrated for an individual charge in figure 35 below. In panel a, a charged particle is forced to oscillate at the
frequency of the incident radiation with dynamics as shown in panel b. The electric field emanating from the charge will exhibit, in addition to an ineluctable radial field, an oscillating transverse component, labeled ESx as shown in panel a, that diminishes less rapidly and will not be cancelled like the outward component will. The transverse component will be oppositely directed from that of the incident field (i.e., out of phase), tending to cancel it as shown in panel c.
Incident electromagnetic radiation will cause the individual electronic charges to experience a Lorentz force that will produce displacements of the charges. Due to their much lighter mass, electrons will experience much greater effects. This force is given by:
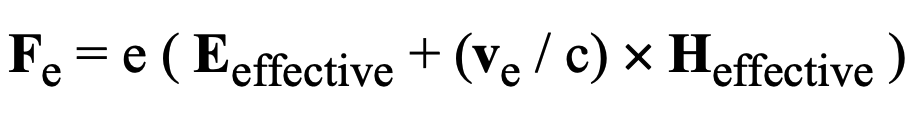
where e = 4.8×10^-10 statcoulombs (in cgs units that we will use throughout) is the individual electronic charge, v_e is the electron’s velocity with respect to an observer of the scattered radiation and the vector operator symbol ‘X’ represents the cross product.
Each electron will experience, in addition to this Lorentz force, restoring and damping forces representing the medium’s ability to restore the locally altered equilibrium and its tendency to dissipate energy. The resulting displacements will be along the x-axis under the assumptions of isotropy and homogeneity of the medium for the example incident radiation shown in figure 34. The formulation of these forces on a single electron is represented by the following differential equation of classical electrodynamics:

where the second and third terms on the right correspond to a proportional restoring force and a velocity-dependent damping force associated, respectively, with the harmonic restoring force on
charges about a stable neutral position and an absorptive effect typically associated with collision probabilities while the incident wave is interacting with the electron, effecting joule heating. These coefficients will determine the magnitude of an inherent resonant frequency of the medium, and the absorption properties to be expected of the medium. The situation is considerably simplified by addressing merely a single resonant frequency; this simplification is appropriate for a fully ionized homogeneous medium in Maxwellian equilibrium. Solution of the previous differential equation results in the displacement formula:
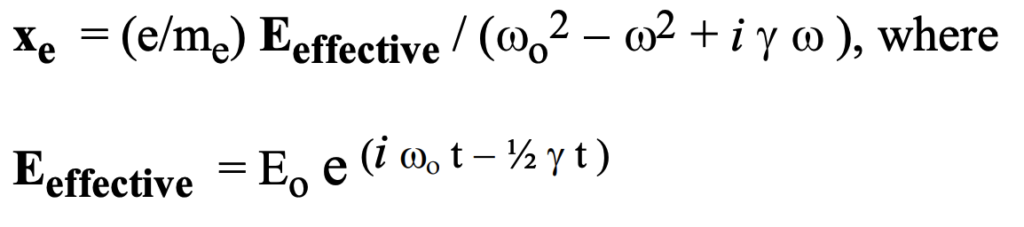
x_e is a displacement that is in direct response to the incident radiation.
Figure 35 illustrates the mechanism whereby the effective field is augmented by these displacements caused by the incident electric field. At some distance removed from the electron that is
affected by the incident radiation field, the electronic charge produces an electric field directed away from the charge. There will be a component of this field E_s that is along the direction of
the incident radiation and a component at right angles to it as shown. The component that is along the direction of propagation will diminish with the distance from the electron according to the usual coulomb inverse square law. However, the transverse component of the field will diminish only as the inverse first power of distance. Thus, after any very appreciable distance E_s will itself comprise transverse radiation that is one quarter wavelength behind that of the incident electromagnetic wave.
As we will see in a later chapter, this scattering radiation from individual electrons in the medium will accumulate by coherent constructive reinforcement until eventually their combined effect is to nullify and replace the incident radiation altogether.
Both the ‘resonant frequency’ w_o and gamma will play key roles in interpreting observations through the intergalactic medium. From the above
equations, we obtain the following:
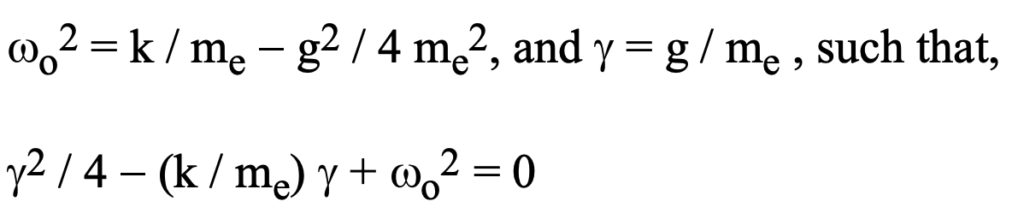
This relation between k, gamma, and w_o is shown in figure 36. It expresses relationships between the force constants and derived parameters that determine scattering behavior. Specifics of the
scattering process determine these important parameters. With regard to the intergalactic medium, estimating gamma based on knowledge of w_o will be of interest in a couple of instances in
particular.
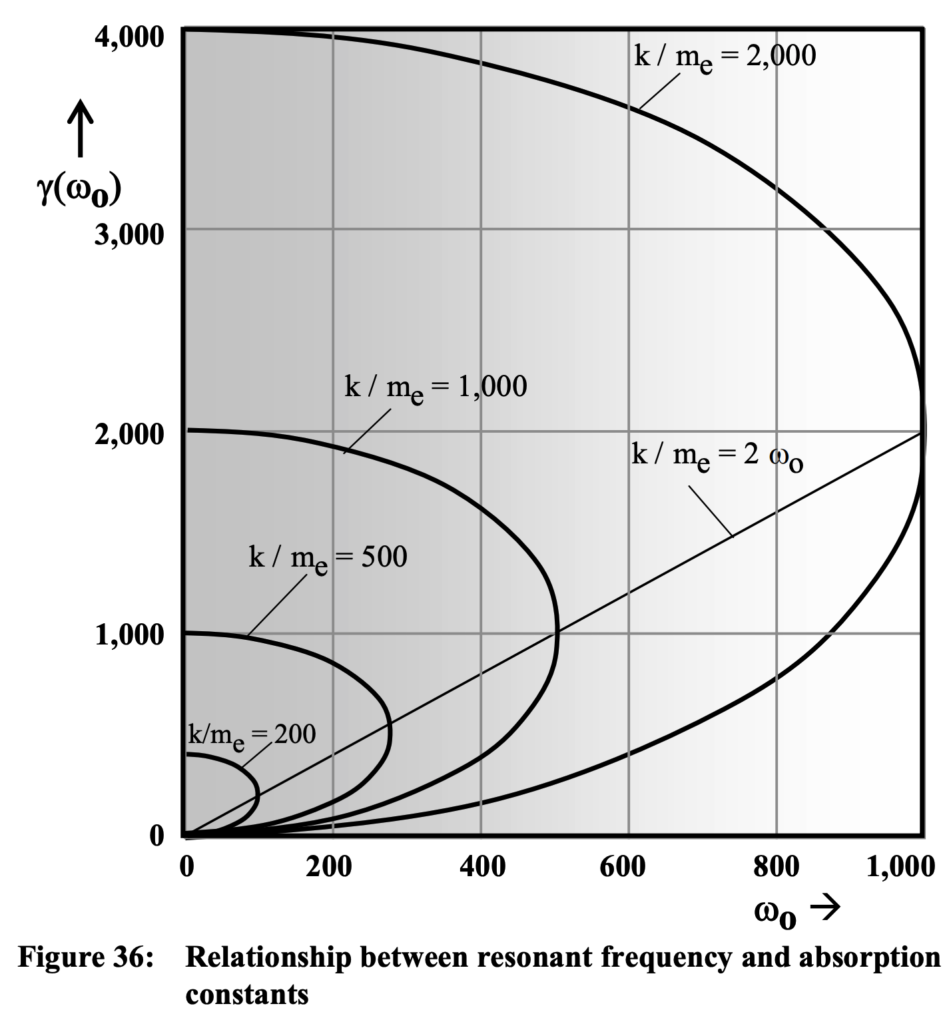
dispersion formulas
The induced dipole moment illustrated in figure 35 is a reaction to the incident force; it is also oriented along the x axis in an isotropic medium as appropriate to the intergalactic medium for wave functions like the one shown in figure 34. The reaction force on a single electron resulting from this displacement is given by:

where P_e is the contribution of a single electron to overall polarization, P, of the entire medium at a given point in space. This is the basic Lorentz-Lorenz formula. The effect on the incident radiation of the interaction with the electronic charges in a material substance is that overall transmission characteristics may be significantly altered by introducing refraction, diffraction, and absorption. This dispersion is also associated with a wavelength dependent propagation velocity of the on-going radiation.
In the Lorentz force equation presented above, the introduction of scattered electric fields resulting from the induced polarization effects on the incident electric field realized throughout the medium is associated with a property called the ‘refractive index’ or ‘index of refraction’, n of the medium. The quantity n was used earlier in the representation of the incident electromagnetic field wave functions. It is in general a complex quantity (i. e., possessing both ‘real’ and ‘imaginary’ components) that determine propagation velocities in the medium as follows:
n = c / b,
where b is the complex speed of light in the medium and c is again the universal ‘real’ speed of light in a vacuum. The ‘phase velocity’ of radiation in the medium is represented by the real part of b and the ‘group velocity’ by its norm. We will continue the dispersion formula derivations in reference to n rather than b as is usual in such discussions. The imaginary part of n determines the absorption properties of the medium.
the Lorentz-Lorenz formula
By further substitution of the derived values we obtained above for P and E_effective into the preceding formula, we obtain. The usual expression that is valid to a very high degree of accuracy, for which the ‘dielectric susceptibility’, (n -1), is assessed as follows:
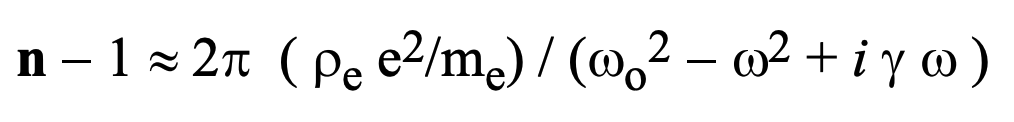
The index of refraction, as we have said, is complex and can be expressed in the form:

where Re(x) and Im(x) refer respectively to exclusively real and imaginary components of a complex argument, x. From the formula for the dielectric susceptibility above, we obtain:
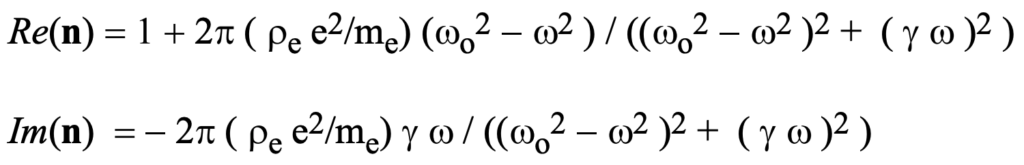
These functions are plotted in figure 37 for nominal parameter values of w_o = gamma = 87, which are what one might naively expect for the intergalactic plasma. The forms of these two curves are quite general, but not without quite extreme domain peculiarities. For examples of the dependence on gamm, for example, see figure 38.
In exploring the ramifications of these formulas, it is clear that behavior will be markedly different if the frequency w of the radiation that is propagated through the medium is higher or lower than the resonant frequency, w_o that is a characteristic of the medium itself.
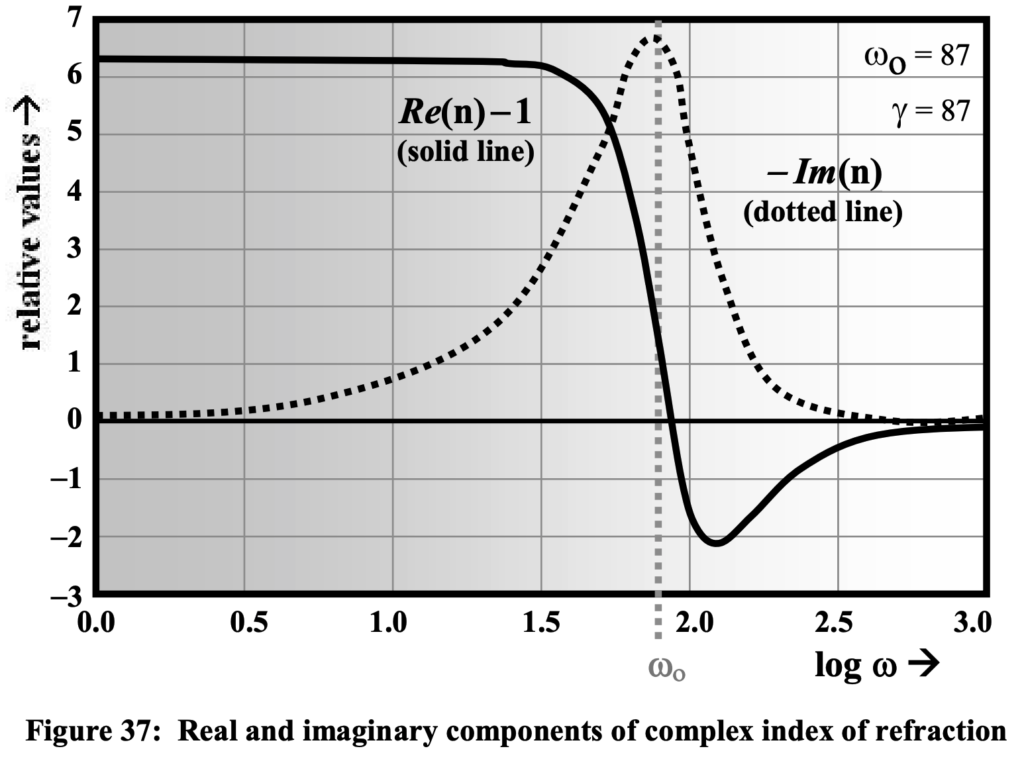
The magnitude and functional form of the index of refraction curves depend not only upon the relative values of gamma and w_o as shown in figure 37, but intimately upon the relationships between and gamma, w, and w_o as well. These dependencies, particularly for the imaginary portion, have a profound effect on the luminosity of objects observed through the medium. It is the imaginary part of this complex index of refraction that affects the amount and nature of the absorption encountered by electromagnetic radiation propagated through such a medium. Counter-intuitively, the larger the value of gamma becomes, the more nearly the medium will behave like a complete vacuum for which Re(n) = 1.0 and Im(n) = 0.0. This is readily apparent in figure 38.
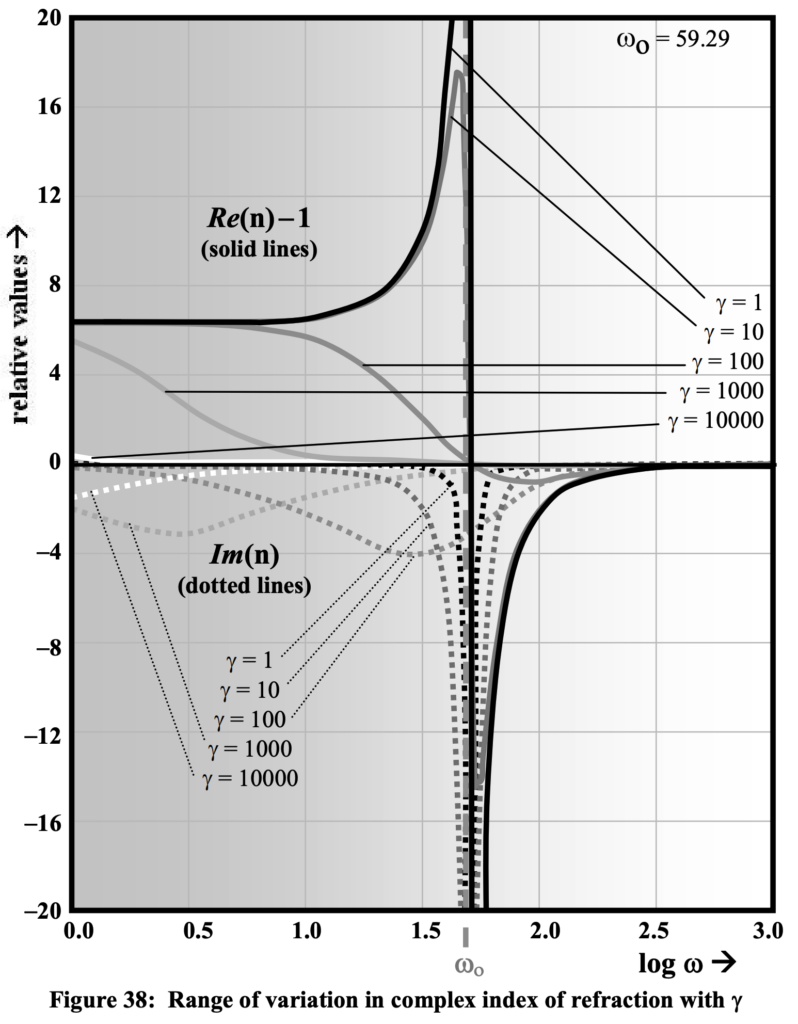
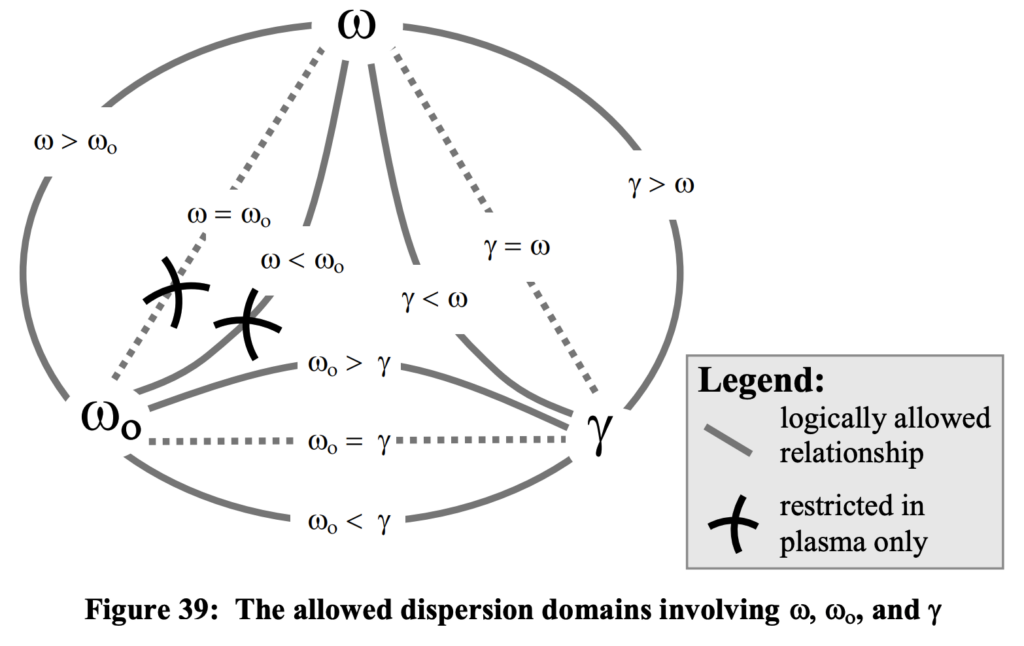
As illustrated in figure 39, there are nine possible domains for which dispersion behavior could be basically different. Clearly, some of these alternatives are of much less consequence than are others. In particular in the vicinity of w = w_o, if gamma is much greater than w and w_o, both functions shown in figure 38 are nearly zero. Furthermore, this quiescent neighborhood can be quite extensive in cases where gamma >> w_o for an extremely large range of values of the incident radiation frequency, w as shown in figure 40. If, for example, gamma is two orders of magnitude greater than w_o, then there will be a neighborhood four orders of magnitude on either side of the resonance frequency in which,
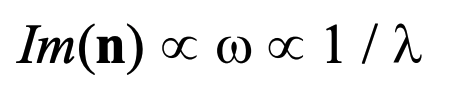
This non-dispersive feature of absorption applicable to plasma is one of the keys to an understanding of how the Hubble relation of the luminosity of objects at cosmological distances is accounted for in the scattering model. However, except for this region in the vicinity of wo (whether vast or small depending on the value of gamma) as described above and shown in figures 40a and 40b, the imaginary component of the index of refraction, and therefore absorption, will be extremely wavelength dependent. This factor will either be proportional to lambda^2 (i. e., 1/w^2 ) for w > w_o or proportional to the inverse of lambda (i. e., to w) if w < w_o.

application of formulas to the intergalactic plasma
In the case of an hydrogenous plasma medium, the domain of applicability of the formula to propagation of electromagnetic radiation is extremely to the high frequency side of w_o , placing this
useful domain far to the right of the right-most value (w= 10^3 Hertz) shown in figures 38 and 39. Since there is virtually complete absorption of radiation at this frequency, we can assume that gamma must tend to zero.
At the frequency w_o there is a Jell-O-like resonance of the medium as a whole in which the transverse wave motion is converted to a longitudinal (sound-like) action. Thus, electromagnetic radiation as such can only propagate through plasma at frequencies greater than this radial plasma frequency, w_o. However, even 100 Megahertz radio signals correspond to values of w that are on the order of 10^9 Hertz — many orders of magnitude greater than w_o. The values of w_o = 87 and 59.29 employed respectively in figures 37 and 38 are more or less directly applicable to intergalactic plasma although the value of gamma is no doubt over-estimated.
At what is known as the ‘plasma frequency’, w_p = w_o, all of the transverse electromagnetic radiation is converted into longitudinal oscillations of the charges within the medium. This ‘radial plasma frequency’, as it is sometimes denominated in this context, is determined by the electron density as follows:
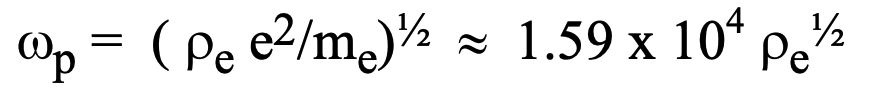
This arrangement of basic parameters appeared independently as a leading factor in the dielectric susceptibility. Substituting values applicable to the intergalactic medium yields the following approximate restriction on the values of this resonant frequency:
2.0 < w_o < 2.0 x 10^3 Hz
So that clearly for optical wavelengths (and for even the longest radio wavelengths currently employed in astronomical observations) there will be no observable spectral line attenuation attributable to this particular resonant frequency of intergalactic plasma. For optical wavelengths around 5000 Angstroms = 5 x 10^5 cm, we have the relationship,

However, we will discover that there is a mechanism operative in hot plasmas whereby scattering by relativistic electrons produces a lengthening of wavelength of all electromagnetic radiation propagated through it. In the plasma scattering model being presented here, a reduction of radiant energy via redshifting results from an angular deflection that, although compensated at each scattering event, is associated with an equivalent amount of energy being removed from the radiation. This ‘removal’ of energy from radiation is, in effect, an absorption by the plasma electrons involved in the scattering. At each interaction in the forward scattering process, we will find that the wavelength is increased by Delta-lambda_emitted = 6.12 x 10^-20 T_e. This is accomplished by a Compton-like transfer mechanism that enforces the conservation of energy and momentum. This mechanism can be described similarly to explanations of other transfer mechanisms, i. e., using values g and therefore gamm_C unique to this process.
Then by summing the contributions to the plasma dielectric susceptibility as discussed in the previous section, we obtain,
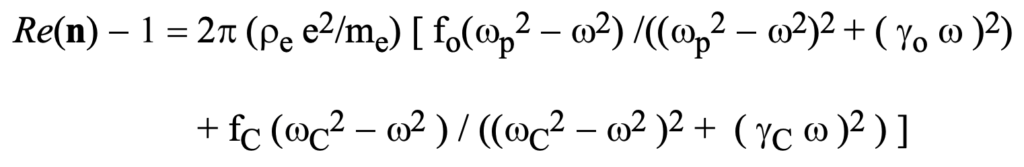
Keeping in mind that gamma_C >> gamma_o, we investigate the case where gamma_C >>w_C is also the case. The final term in the bracketed factor will always be negligible in comparison with the first, so it can be ignored throughout the extensive range for which w_C << w.
On the other hand with regard to the imaginary component, a very different situation arises, where we obtain:
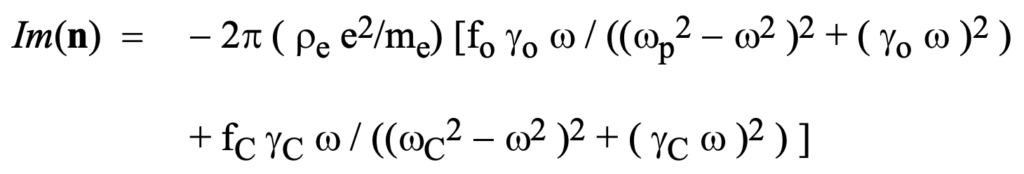
In this case, where we again assume that gamma_C >> gamma_o, the second term will take on primary significance. First of all, the assumption is warranted because gamma_o must be very nearly zero in order to effect the virtually complete absorption by the plasma resonance mechanism. So let us look at the range of possibilities for the frequency dependence of this second term. In figure 41 we illustrate the range of possibilities for the relationships between and among the parameters pertinent to absorption, gamma_C, w_C, and w:
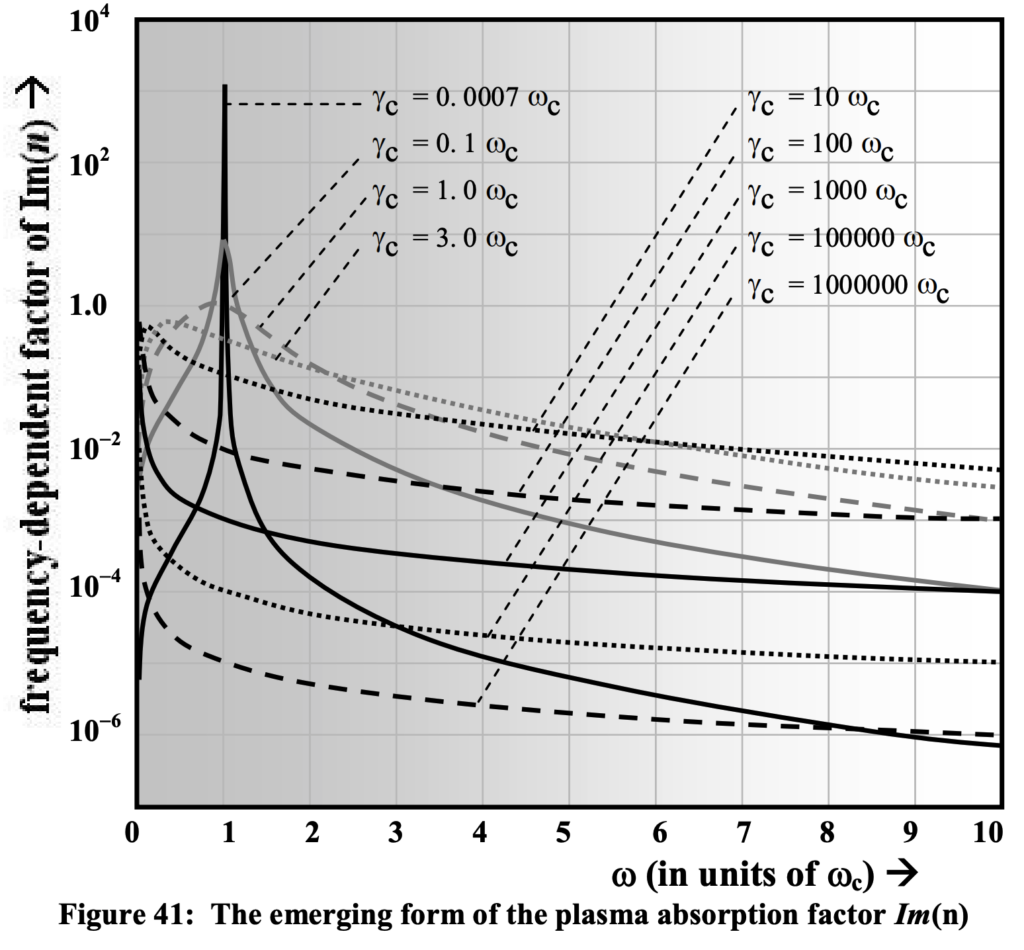
Since the mechanism of wavelength lengthening to be described later in this volume is unilateral for all wavelengths, therefore, the energy absorbed as an integral aspect of this mechanism must be extremely broadband throughout an extremely extensive region of the electromagnetic spectrum. As shown in figure 41, this broadband feature is accommodated when gamma_C >> w_C. There is no rationale for w_C having a value other than w_p, which is extremely small as we have seen. This form of plasma-determined absorption will, therefore, remain exclusively dependent on the second term in the bracketed factor of Im(n) above, as long as we also have that gamma_C >> w.
Therefore, throughout a broad range of the electromagnetic spectrum we can characterize the index of refraction of intergalactic plasma as follows:

In an attempt to obtain a value for gamma_C, we note that based on later results, the observed redshifting effect and energy balance equations will be maintained if (on average) the following holds:
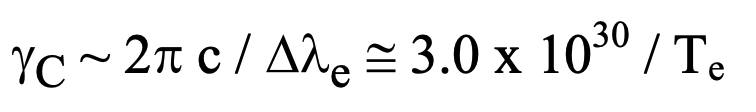
Therefore, for electromagnetic radiations with which we will be interested, the plasma parameters in the Lorentz-Lorenz dispersion formulas assure that the index of refraction of the intergalactic medium will be approximately n = 1.0 that is almost identical to what would be appropriate to a vacuum. Only at what are considered ‘cosmological’ distances will its effects be otherwise observed. For visible light, component values are on the order of: |Re(n) – 1| ~ 10^-38 and |Im(n)| ~ 10^-37.
For the domain of parameters appropriate for application to the intergalactic plasma, the real part of the index of refraction is actually less than unity as shown in figures 37 and 38. This corresponds to the phase (as against group) velocity of a wave that exceeds the speed c. Of course the speed of transference of energy via electromagnetic radiation will be determined from the norm of the complex index of refraction, not just the real part. The norm will always produce an actual group velocity that will not exceed c. However, only for extremely low frequencies approaching the plasma wavelength (lambda_o = 2 pi c / w_o ~ 2 x 10^9 cm), at which wavelength the transverse electromagnetic radiating energy is absorbed and converted into longitudinal oscillations of the plasma charges, would one expect anomalous dispersion to become an appreciably observable local phenomenon.
As illustrated in figure 40, there are two families of curves for the two distinct domains on opposite sides of w = w_o. Certainly, gamma_C >> w_o recommends itself as what must pertain to produce the observed broadband behavior. On the other hand, the fact that there must be complete absorption at w_o suggests that gamma_o << w_o must pertain. Accepting this criterion with gamma_o ~ 0 accommodates the maximal absorption at w < or = w_o as well as accommodating the minimal absorption for all shorter wavelengths. Thus there are two concurrent operative processes in the plasma.
What is at issue in integrating these very different alternatives? Values of gamma are typically experimentally determined since they involve intricacies of the mechanisms. If the primary
operative phenomenon was plasma resonance, clearly the steep functionality of Im(n) proportional to 1 / w^3 appropriate to gamma < w < w_o would precipitate no absorption of radiation at shorter wavelengths.
However, in addition to the plasma being a plasma with its own unique resonance, there is a very different additional dispersion process that takes place in a ‘hot’ plasma, the exploration and ramifications of which are what succeeding posts will be about. There is a completely unique forward scattering process applicable to extremely high temperature plasma that results in the redshifting of any radiation that propagates through it. The stealing of energy that is immeasurable in any single scattering interaction is nonetheless an ineluctable energy siphoning mechanism whose effects are magnified by coherent forward scattering as we will demonstrate.
Leave a Reply