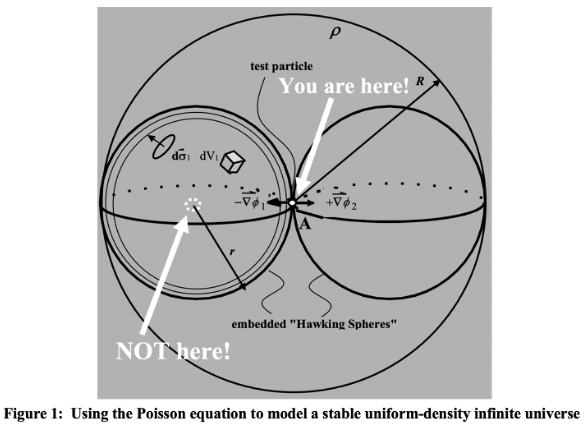
The Poisson equation was at issue in the centuries long debate about whether an infinite stationary state universe would collapse under its own weight. It describes the behavior of a classical gravitational system; an analogous equation describes behavior in general relativity. Einstein ran afoul in his analyses because Poisson’s equation is not just an equation; it is the formulation of a ‘boundary value problem’. The equation applies within specified boundary conditions of the system under consideration. Newton had argued that no boundary to an infinitely distance assured there would be no collapse. But Einstein and Hawking modeled an infinite spherical universe as circumscribed by a spherical boundary, albeit at an infinite distance in the limit. But their model features an inside and an illegitimate outside of the universe.
There is no ‘outside’ of an infinite universe. However large the three-dimensional sphere one chooses to represent an infinite universe (refer to the ones of increasing size on the left in figure 1 showing attempts to increase it without limit), there is an equally, increasingly large adjacent spherical region which is also a part of an infinite universe. All the rest of an infinite universe (both inside and outside the larger sphere) is symmetric about that central point of contact of the two smaller spheres where gravitational collapse would begin. All gravitational forces at every point on the surface of the smaller sphere cancel so there can be no collapse in a uniformly dense infinite universe. It is Einstein’s and Hawking’s model, not Poisson’s equation, that is incorrect.
Certainly gravitational collapse into stars, galaxies, and galaxy clusters is observed. Over (and under) densities certainly will and do occur for various reasons throughout an otherwise uniformly dense universe. In over densities gravitational effects will produce contraction into gravitationally bound systems as shown in figure 2. But such over densities do not precipitate overall collapse.
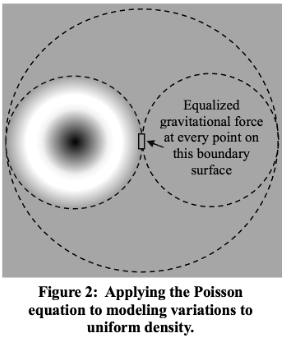
Notwithstanding emphasis placed on it, gravity is not the only ‘force’ to be considered in analyses of variations on the distributions of matter in an infinite universe that is uniformly dense at the highest level. Thermodynamic considerations must be taken into account as well. Any volume of particulate matter at a temperature above absolute zero experiences an outward pressure that would, if unconstrained, force continued outward expansion in accordance with the traditional ideal gas thermodynamic formula:
P V = n k T
where P is thermodynamic pressure, V is the volume within the boundary surface, n is the number of the particles of gas within the volume, so the average particle density is n/V. The parameter k = 1.38 x 10-16 erg sec is Boltzmann’s constant and T is the average temperature of the gas within the volume in units of kelvins K.
This outward thermodynamic pressure at the surface associated with the force fP in figure 3 would be countered by the gravitational force fg of the matter contained within the volume as was assumed by Einstein’s initial conclusion of a collapsing universe without counterbalance. This gravitational force would increase the local density, raising the kinetic temperature, and thereby further increasing the balancing outward pressure.
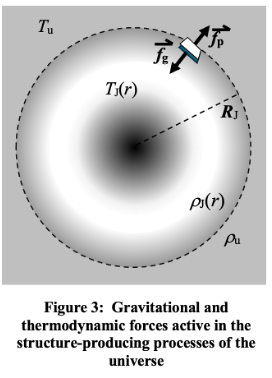
The Jeans criterion for collapse takes both these forces into account in assessing conditions throughout the volume for overall stability. The Jeans Collapse Criterion is a specification of the situation in which these two forces are equal and opposite. If a region of gas is compressed within a region of radius RJ defined as the Jeans radius the gravitational force of the enclosed mass will exceed the outward pressure causing the gas to collapse further.
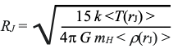
This Jeans radius is the dimension of a spherically symmetric region where counter forces are equal, and the size of the region will remain stable. In a hydrogenous plasma the average mass of the particles is mH = 1.67 x 10-24 gm, the average density <rho(r)> = n mH /V(r) and V(r) = 4/3 pi RJ3. To balance gravitational forces, the average mass density of the encapsulated stable over density < rhoJ(r) > must equal the average mass density of the universe as was shown in figure 2. The brackets “< >” are used to denoted the average of the enclosed parameter values. This density is on the order of rhou » 10-30 gm/cm3 although this value depends on assumptions about dark matter. The gravitational constant is G = 6.674 x 10-8 cm3/gm sec2. Thus, we obtain:
RJ = 1.22 x 1024 ( <T > )1/2 cm
The average temperature throughout the region within the Jeans radius must equal the average temperature throughout the universe if the universe is to remain in balance thermodynamically as well as gravitationally, which it must. There are considerable reasons to conclude that this temperature is bounded by 103 < Tu < 104, not least of which are observationally validated plots of temperature and density throughout galaxy cluster over density regions out to the boundaries between them. See plots based on the beta model of galaxy cluster plasma gas data in figure 4 where the radii are in units of Mpc = 3.07 x 1024 cm or 3.26 x 106 light year, and the electron (number of baryons) density provided in the figure is rho(r) = rhoJ(r) / 1.673 x 10-24, converting mass density into baryon (and electron) density.
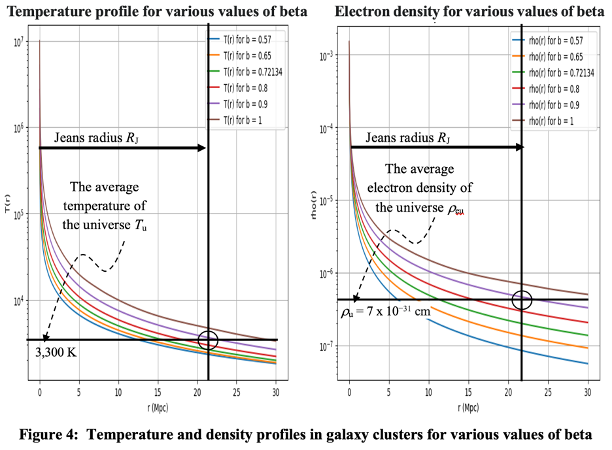
These values of temperature and density are ballpark values, but they are collaborated by other observations and analyses described in various papers on the author’s site. It is interesting although coincidental that the standard cosmological model posits the origin of the CMB at a surface of last scattering at a temperature of about 3,300 K; this value is also compatible with the origin of the CMB in the author’s stationary state scattering model. This value results in the following value of the Jeans radius:
RJ = 6.75 x 1025 cm = 22 Mpc
MJ = (4/3) pi RJ3 <rhoJ(RJ)> = 1.29 x 1078 x 7 x 10-31 = 9 x 1047 gm
In units of solar mass MO = 2 x 1033 gm, we have:
MJO = MJ / 2 x 1033 = 4.5 x 1014 MO
It is noteworthy that the masses of galaxy clusters fall within the range:
1014 MO < MJ < 1015 MO
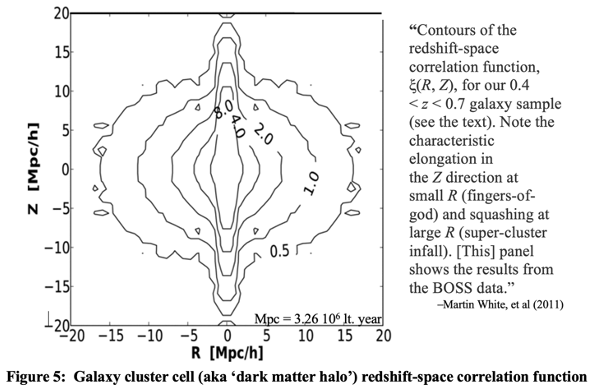
The stable over densities are obviously the observed galaxy cluster cells, structural components at the largest scale of a stationary state universe with their lower level collapsed eddies of plasma gases becoming host galaxies for stars. They exhibit broad redshift variation of their galaxies as shown by White, et al. in figure 5. This variation is not just a reflection of virial motions but an inherent dependence on plasma density of surrounding the galaxies orbiting about their centers. Clusters are not all the same size but are very nearly so as clearly suggested by BOSS data of galaxy surveys. Notice the similarity of dimensions in White’s observations to our determination of RJ. That the attributed numbers of observed galaxies per cluster vary so broadly has more to do with cell alignment and their variance in redshift when observing through them than on the physical allocation of galaxies in each cell.
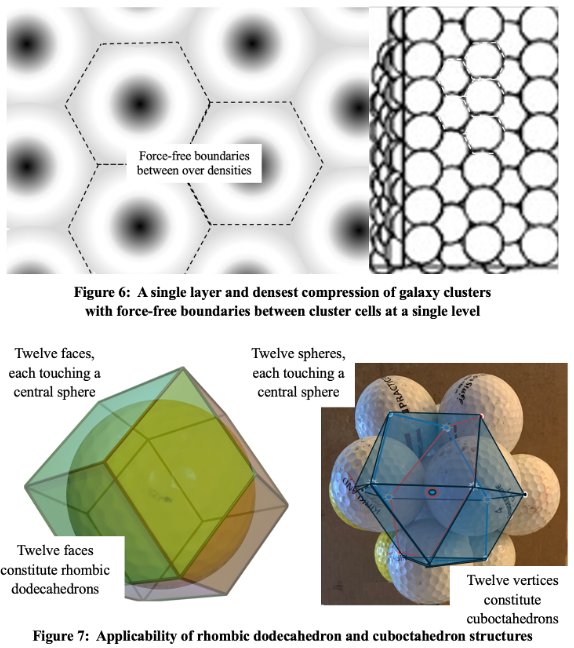
At the borders between cluster cells the requisite universal averages of temperature and density are realized. There is a Voronoi tessellation of space as each cell abuts adjacent cluster cells with zero force boundaries. This involves a closest ‘packing’ in space, whose two-dimensional organization is very much like that shown in figure 6. In three dimensions, these force free boundaries that entomb the cluster cell would for identically sized cells constitute twelve-sided rhombic dodecahedrons. Each face is the face of another cluster cell rhombus forming a cuboctahedron of 13 total cells including the one at the center; both these solid shapes are capable of completely tessellating space. These structures are shown in figure 7.
We have ignored conventional distinctions between baryonic and ‘dark’ matter, not because it doesn’t matter, but because it does. The distorted emphasis on gravitation as the primary determinant of cosmological effects resulted in the introduction of unseen and nonelectrodynamically interactive matter. That is because gravity applied to the only kind of matter that is scientifically understood would be insufficient to accounting for much of what is observed of the cosmos. The very definition of dark matter precludes its incorporation into any thermalization processes that counterbalance gravitational collapse because those processes are driven by electromagnetic interactions with baryonic matter. It is thermodynamics to an even greater extent than gravitation that is required in modeling the real stationary state of our universe — most particularly the generation and propagation of the CMB. With its complete incorporation dark matter is unnecessary and anathema. And entropy is not how it all ends, it is rather the driving force that keeps it going – yes, even forever.
We have come full circle. Initially there was Einstein’s disagreement with Newton concerning the stability of an infinite universe. Then his analogy of an expanding balloon with coins stuck on it to represent galaxy clusters that in themselves were seen as having nothing at all to do with major cosmological issues including cosmological redshift, and the supposed origin and expansion of the universe – created and emerging from nothing. But here we are. We have found that expansion is not required as a mechanism to result in redshift, to keep an infinite universe from collapsing in upon itself, nor is it required as a cause of the observed cosmological redshift. Galaxy cluster cells contain all the secrets of the entire universe that is comprised completely of them. The inferred average baryonic mass density and average kinetic temperature, in agreement with the average kinetic and radiation energy density and temperature of the cosmic microwave background (CMB), all of which characterizes the universe. See related articles describing the analyses and discoveries that describe the nature of and mechanisms that produce these realities. These papers are archived under the heading ‘cosmology papers’ on the author’s web site at https://fred.vaughan.cc/scientific/cosmology-papers/.
Leave a Reply