Quark Soup Recipes

That’s pretty much the party line. Such statements presume a temperature (and time) when subatomic particle creation took place. But the process is described in reverse order as if baryons create the soup rather than the soup creating the baryons. And what about the electrons? What do they release? Are they in the soup too? Such descriptions are not informative with regard to a determination of how the quark soup is created. There must be ingredients that exist at the extreme temperatures that result in the cooked soup that subsequently (and at lower temperatures) ‘freezes’ into the protons, neutrons, and electrons that populate our world. So, rather than looking at the physical implications of increased temperature on viable mundane structures of matter and energy, let’s look at the implications of high energy photons at extreme temperatures that result in the stuff that will ultimately beautify the periodic table.

Would a quark soup have been primordial – the ‘beginning’ – like the ingredients one buys in a grocery store that grow on trees or are dug up out of the ground ready to be cooked, or are quarks created from something else that has to be cooked in order to create the table-ready dish? We’ll need to consider what we mean by ‘beginning’ as we loosen our hold on the Big Bang. Is the intention of ‘beginning’ to be an early epoch of cosmogony like a scientific ‘station of the cross,’ or is it rather a logical precursor in the sense of a scientific assessment of the state of matter and energy at the various temperatures that occur in an expanding or a stationary state universe? I lean toward the latter; I like my coffee black.

So let’s try to make sense of this quark soup and what are the physical prerequisites for creating it.

Beginning at the logical beginning, we must address the most basic concept, E = m c². Everyone is by now familiar with that simple equation. It has been burned into our brains by nuclear holocausts that have occurred and fears that they might again. Like all knowledge, it is dangerous in the wrong human hands. But its utility is not the epitome of knowledge. There is ample reason to understand the universe whether it makes a profit, wins a war, or makes us feel smug about ourselves – or not.

So consider what E_m = m c² as an equivalence between energy and matter really means. It suggests that there is traffic between the more continuous photon energy, E_p = h c T / lambda, where lambda is the wavelength of a photon, that can transition to particulate matter and the other way around. It is these transitions that we seek to understand.

In a thermodynamic system in equilibrium, the material particulate and radiation photon energies balance. As a system is heated radio waves give way to infrared radiation, then visible light, ultraviolet light, x-rays, and ultimately gamma rays. There is a characteristic predominant wavelength of radiation at every temperature. The number density n_gamma of these photons is extremely dependent on temperature as follows:

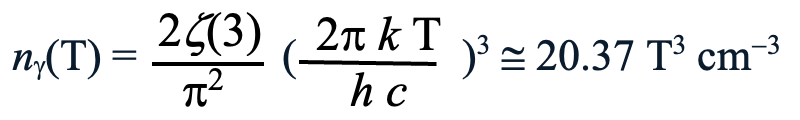
The Riemann zeta function for the value three is a fixed number, ζ(3) ≈ 1.2020569. At 3,000 K, which is an estimate of the average kinetic temperature of the universe, at which n_gamma ≈ 5.5 x 10¹¹ cm^–³. The density of photons is so highly dependence on temperature that, for example, n_gamma(T = 10¹¹) ≈ 2.0 x 10³⁴ cm^–³.

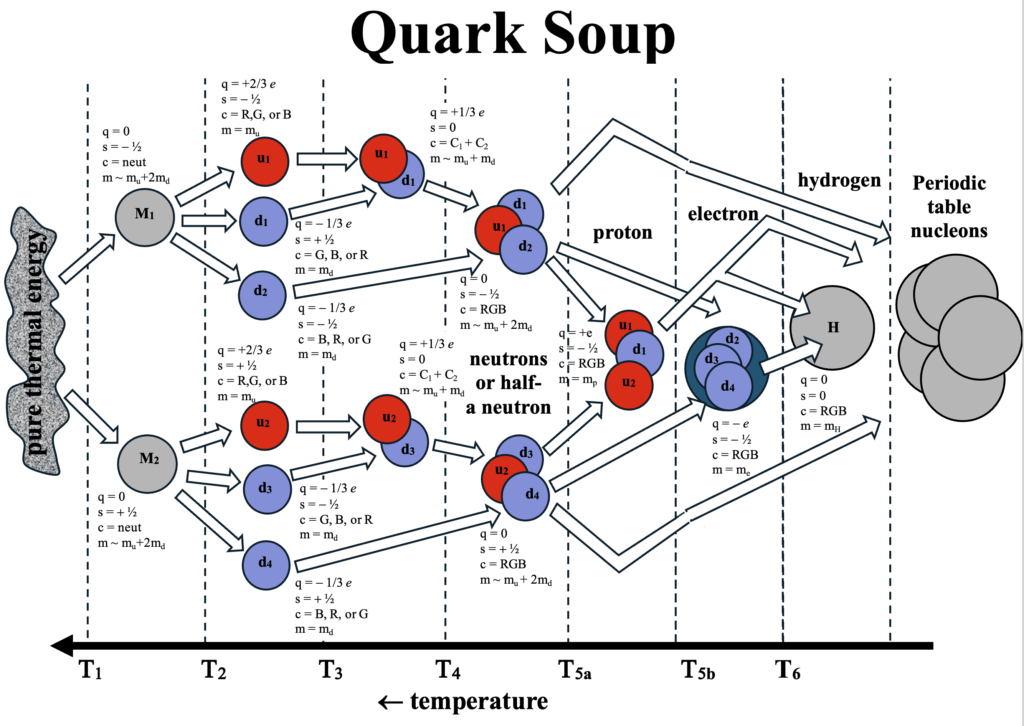
It is a bit counter intuitive that as photon energies increase with temperature, so also does the density of photons. In contrast to radiant energy there are characteristically more particles at lower temperatures. The current average baryon mass density of the universe is estimated at r_m ≈ 2 to 4 x 10^–³¹ g cm^–³. Since the baryon mass is m_p ≈ 1.67 x 10^–²⁵ g, the average number density of baryons, n_b would currently be between 1.2 and 2.4 x 10^–⁷ cm^–³. A current estimate of the ratio of number densities of baryons to that of photons, eta = n_b / n_g is 4 x 10^–¹⁹. This ratio of number densities of particles and photons plays a major role in the determination of T₁ in the creation of quark soup shown in the following diagram. However, the accuracy of these estimates of the current averages of the universe do not have a major impact as shown in the two following charts.

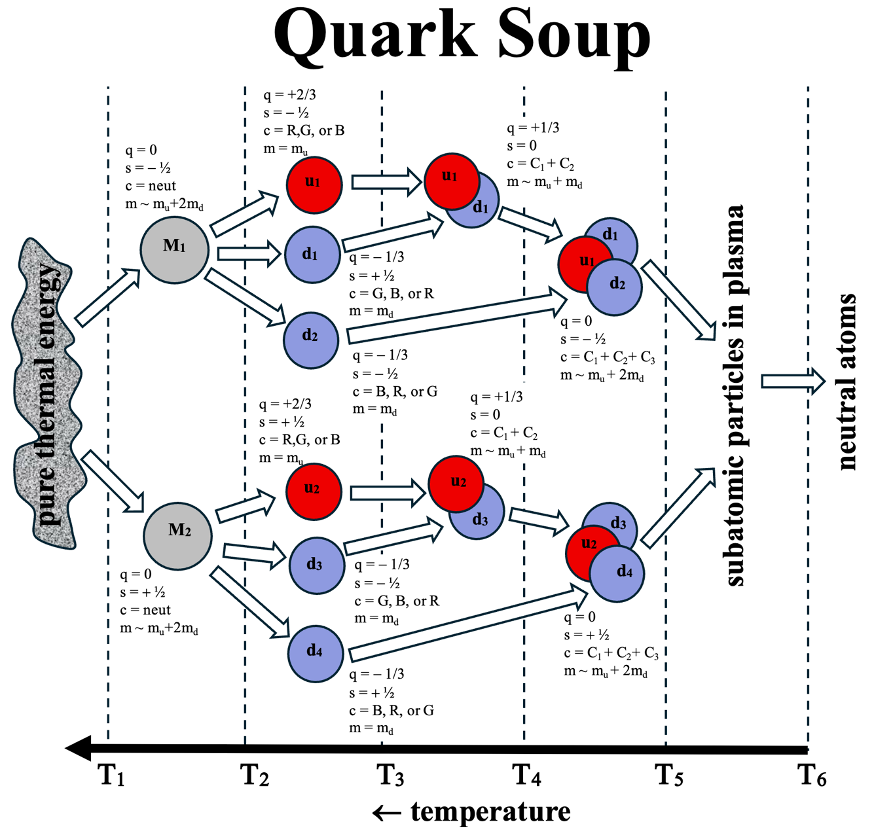
In a stationary state universe, total energy density remains unchanged, but a ‘stationary’ state universe is not static. The universe is rife with hot spots and hot times with energy transitioning between the two forms at critical temperatures T_i when transition criteria are met. A pure energy thermal bath of photons can produce non-identical twin fermion particles, each with mass m_M, that enables a reversible reaction,

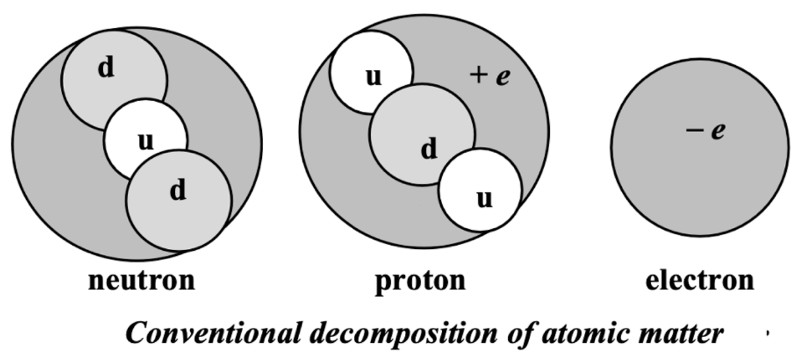
M <–> u + d + d,

which then cascades onward to what we know as the elements of the periodic table. A value of m_M must be on the order of m_u + 2 m_d to enable the reaction that creates the up quark, u, and the two down quarks, d. Each M particle shown at the left of the diagram (above) is ultimately the source of the N_B baryons at the right, so the number density of M particles must be n_M = n_b / N_B for a stationary state. N_B will be unity in most cosmology models because the udd structures at right constitute the traditional neutron (minus the foregone gluon) but in another alternative favored by the author, these structures contain only half of the components of a neutron as discussed in the previous post and elsewhere on this site, so N_B = 0.5.

For this conversion of the thermal photon energy bath to create the M particles and the continued chain on down to the baryon structures of which the current density is n_b, the thermal energy k T₁ must be on the order of m_M c². That relationship is quantified by a Maxwell-Boltzmann/Saha (MB/S) estimate using an intermediate parameter, x_M = m_M c² / k T₁, where,

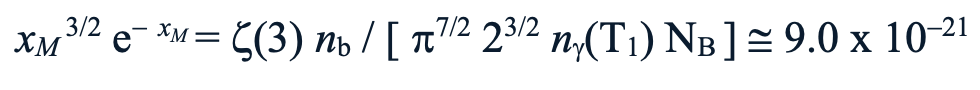
There is a Lambert-W expression that gives a closed form solution, so a value has been determined for x_M based on the number densities discussed above with N_B = 1. In which case the solution is x_M ~= 52, and,

The following Maxwell-Boltzmann (MB) statistics relations apply in obtaining up and down quark densities resulting from the reversible reaction from M.

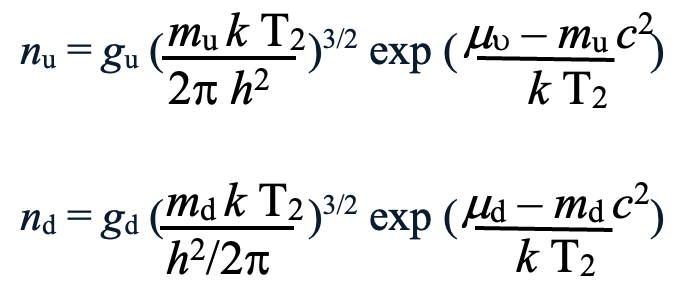
Here g_i = 6 is the degeneracy (charge and color alternatives) of both the up and down quarks, and mu_i is the chemical potential of the free quarks, which in these cases is zero.

The MB law of mass action is used to obtain the temperature at which multiple entities combine to form a single one, e.g. u + d <–> (ud),

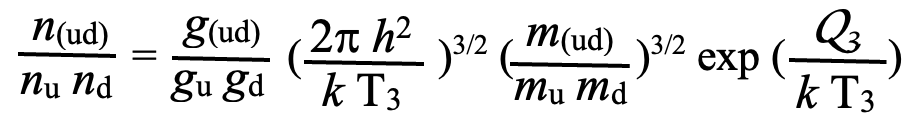
Here the Q – value is the rest-mass (energy) difference on one side of the interaction to the other. (NOTE: this Q is not electric charge!) This will be positive if the reaction releases energy to the right in the relation expression, as it does in this case. This is also the case for d + (ud) <–> (dud). But the inverse is required in the case of (dud) + (dud) <–> p + e.

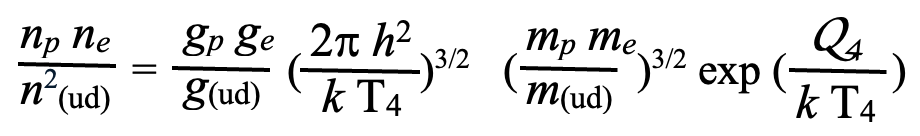
Brief summary of what each of the T_is referenced in the previous quark soup diagram control:

T₁: The temperature at which the thermal bath can efficiently populate parents M (set by the mass m_M and the ratio η/N_B as an anchor of further reactions).

T₂: The equilibrium crossover temperature for M <-> u+2d. Depends on E_M − E_u− 2Ed and degeneracy values g_i).

T₃: The equilibrium crossover temperature for u + d <-> (ud). Depends on the binding energy B_ud, reducing the equilibrium temperature. In general binding energy of two Poisson distributions is determined as the integral of the density of one distribution times the potential of the other:

T₄: The equilibrium crossover temperature for (ud) + d <-> (dud). Depends on ΔB ≡ B_udd− B_ud.

T₅: The recombination temperature for quarks in 2 (dud) <-> (udu) + (ddd) as representing the transition to p + e, where d + d + d => e literally in Alternative #2. Depends on the exponential Q-value, Q = 2 E_dud − (m_p c² + m_e c²).

T₆: The hydrogen recombination temperature for p + e <-> H at a 50–50 neutral hydrogen fraction via the Saha relation (depends on n_b, not on quark parameters).

The specifics of these transition temperatures depend on the assumed structure of the neutron and electron in the two most distinct alternatives we illustrate in detail. Differences are also associated with the differences in masses assigned to the up and down quarks and the treatment of the ratio of the number densities of up and down quarks. The first alternative is linked more closely to the standard model. Thus, in alternative #1, this ratio is not constant because it incorporates transmutation of an up to a down quark – apparently no reverse transmutation is assumed. In the other major alternative this ratio is constant with up and down quarks immutable, the electron is a unification of the three left over down quarks in the reaction creating the proton that satisfies spin and color constraints.

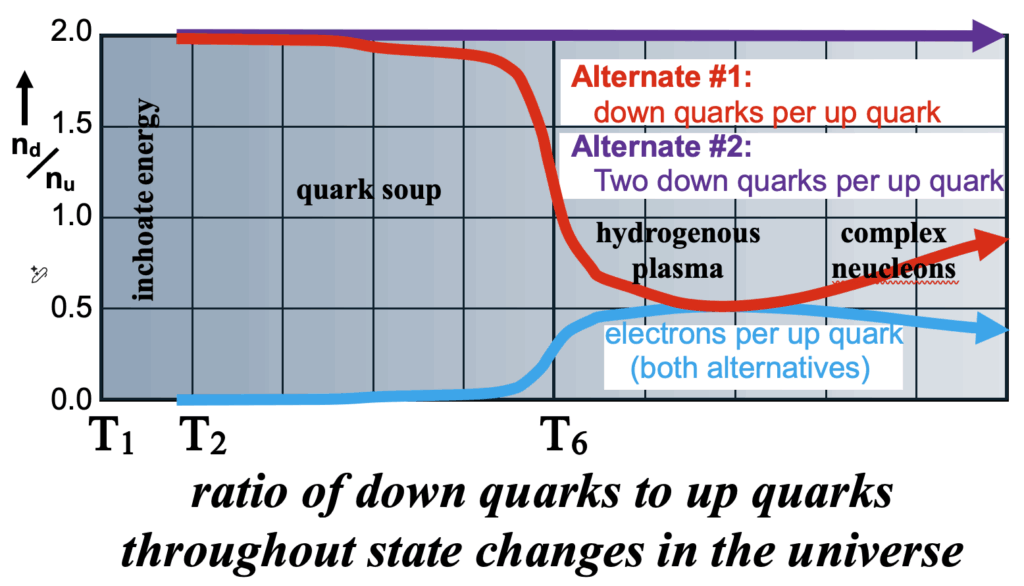
Both alternatives that we will discuss assume a stationary state universe, although for alternate #1 the apparent irreversibility of down quark reductions poses a problem. Poisson distribution of electric charges is the primary source of binding energies in both alternatives based on the characteristic features of the Poisson charge distribution discussed in detail in the previous post:

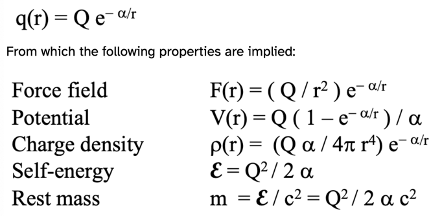
The charges Q are Q_u = 2/3 e and Q_d = 1/3 e, where e = 4.8 x 10^-10 Stat Coulombs. Spin and color assignments are traditional. All alternatives assumed a stationary state universe although the first will have an accumulation of electrons and a variable ratio of up and down quarks..

In a first iteration in both alternatives you will note that the temperatures 1 through 6 do not cascade realistically. It’s herky jerky to say the least. This is due to the exclusive dependence on Poisson electric-only binding energies between quark charge distributions. To fine tune the alternatives analogous to the ‘strong force’ or Yukawa adjustments to the standard model, we have included additional short-range attractive Poisson-distributed kernel potentials:

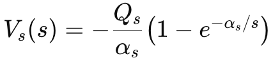
With Q_s a relatively much smaller Stat Coulomb equivalent charge and alpha much smaller than that of the associated quark. This increases B_ud without appreciably altering external effects.

Alternative #1 embraces the quark arrangement assumed in the standard model, but without the gluon, we use N_B =1 because each M particle creates one baryon. The electric charge Poisson distribution parameters are as follows:

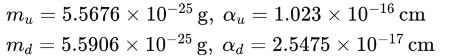
On the first iteration, we obtained the following temperature sequence, hardly the cascade that had been anticipated:

Adjustments were made by applying the central kernel Poisson distribution, resulting in:

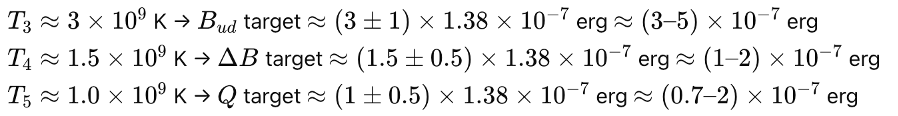
Alternative #1 embraces a very different quark arrangement of the neutron and electron than assumed by the standard model and alternative #1. We use N_B = ½ to avoid the traditional neutron composition requiring transmutation of the up quark, thus altering the ratio of up and down quarks and denying the stationary state. To avoid those perceived problems, in alternative #2 the traditional neutron mass is made up of a doublet of the traditional structure (m_(dud) = ½ m_n) and a conversion/collapse of the three extra down quarks obtained in the proton production then merge to constitute the electron. This requires quite different mass variance assignments to the up and down quarks and different binding energies:

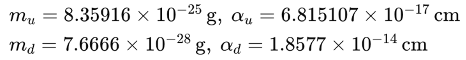
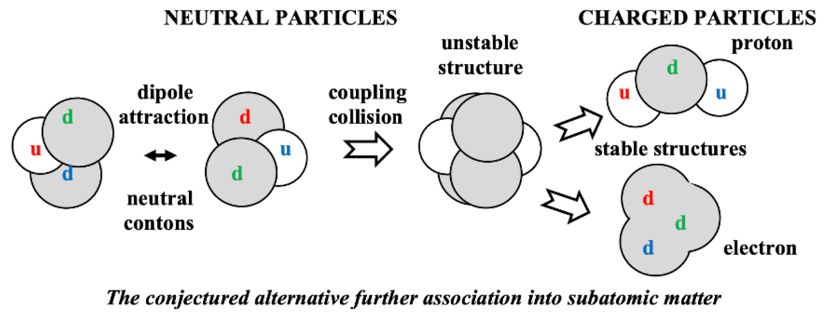
On the first iteration, the same kernel adjustments are required for T₁ through T₅ as for alternative #1.

On the final (for now) iteration, the N_B = ½ was enforced more rigorously as well as the constraint of the electron as a three-down-quark entity from which the following cascade of temperatures was obtained: