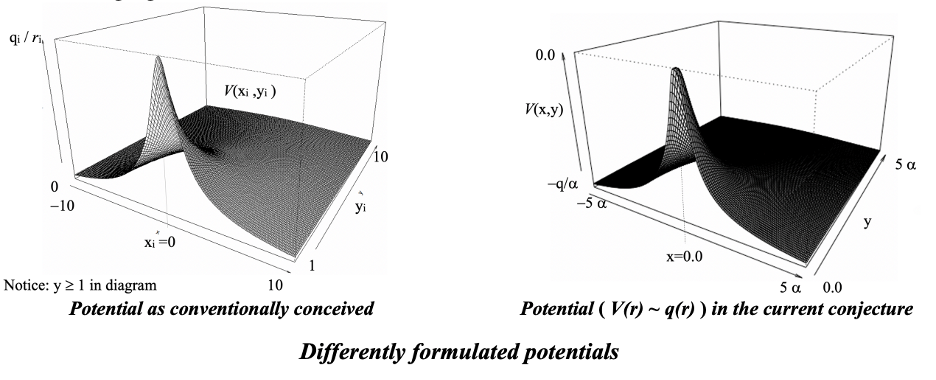
At a distance r away from a spherical charge distribution a force field will be present that is directly proportional to the total amount of charge q(r) contained within the radius r of the center of the distribution and inversely proportional to the square of the distance from the center. There is no way of knowing whether all of that charge is concentrated at the point at the center even though the force is equivalent to that being the case. Alternatively, the force could be due to the total amount of charge being equally distributed at single spherical surfaces between the center and the position at which the force is measured. Or the total amount of the charge could be spread across many spherical surfaces filling the entire volume out to the distance r. There is no discernable difference.
Constituents of charge are infinitesimal up and down quarks confined to subatomic regions of space where direct observation is impossible. It is equally impossible to deny their existence due to consistency with all we accept as true about the universe.
Let’s assume the fundamental charges in quark particles are spherically distributed, with total charge Q; their enclosed charge q(r) is the sum over shells of uniform charge density r(r) out to the distance from the center, r. This can be stated as:
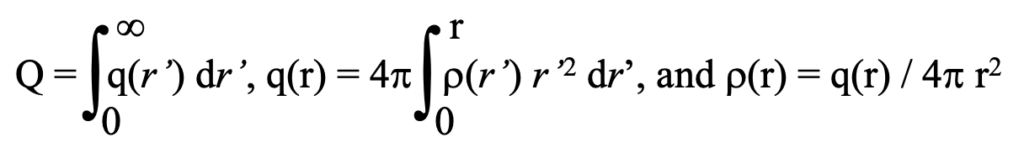
Q is the total amount of charge in the distribution, q(r) is the amount of charge out to the distance r from the center, and 4pi r2r(r) is the total amount of charge in the shell at the distance r. The charge density is the amount of charge at a location a distance r from the center of the distribution.
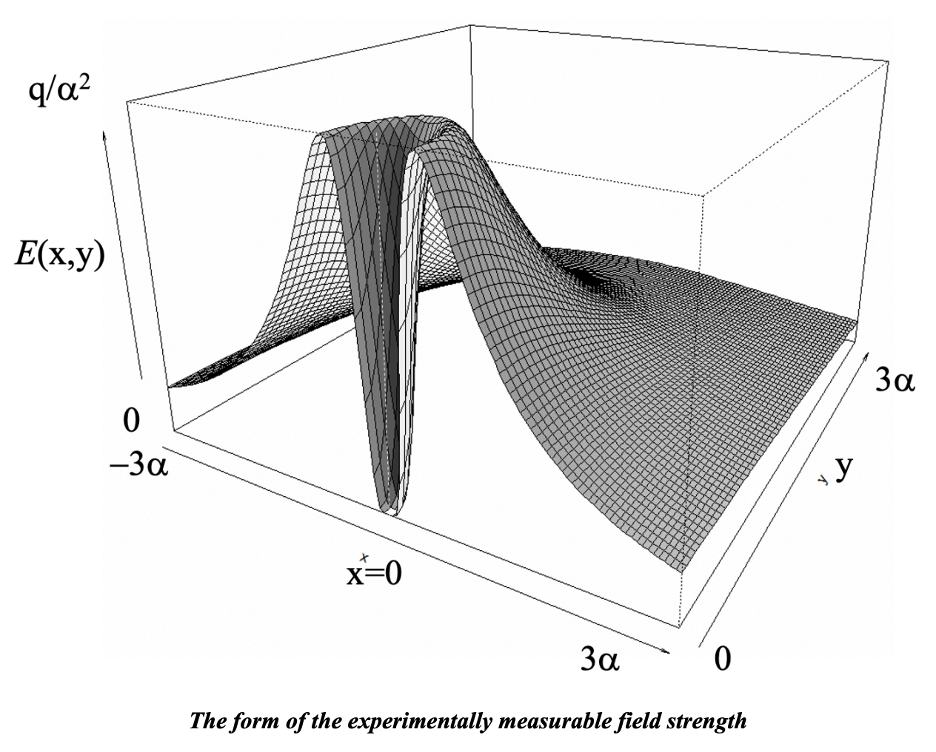
The outwardly directed force field of the ‘particle’ can be characterized as: F(r) = q(r) / r2. This field is minus the gradient of a potential V(r):
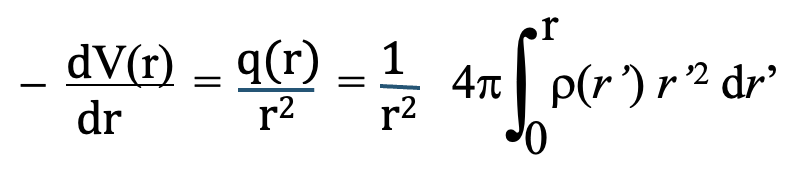
Given the reasonable boundary conditions at the center and at infinite distances from the center, the charge distribution that solves these equations is:
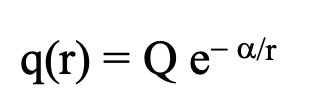
From which the following properties are implied:
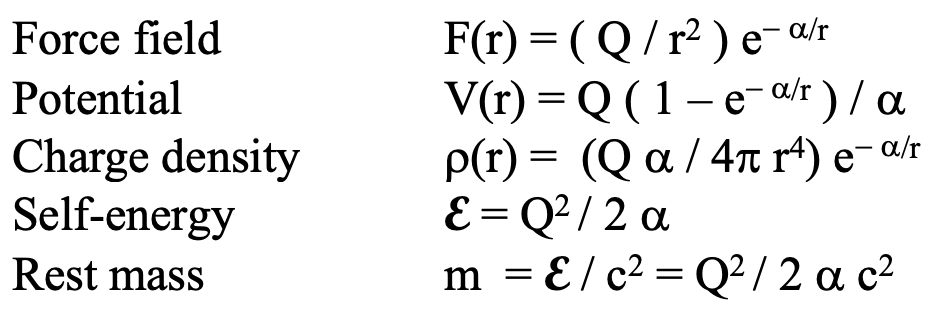


If we assume electric enforcement of confinement distances of quarks with the gluon unnecessary in this scheme, we obtain the following constraint based on the mass of the proton according to conventional decompositions:
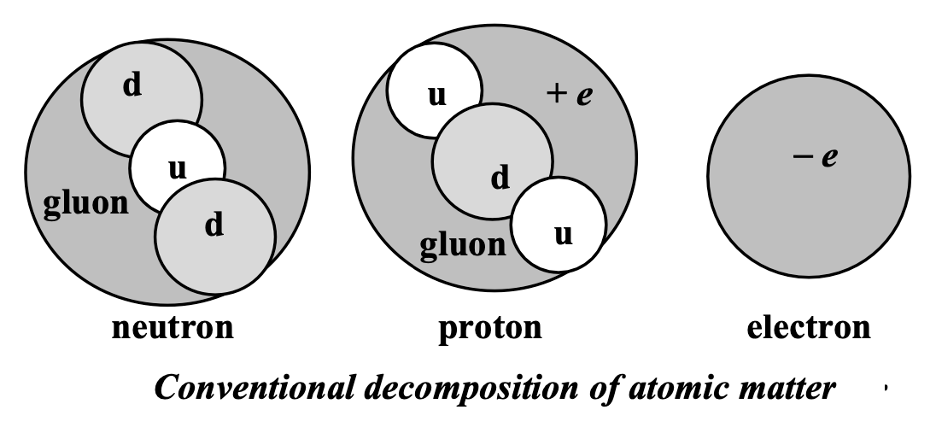
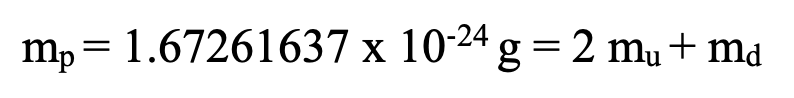
For the neutron we obtain:

Solving these two equations that ignore the mass of the gluon[1] for the two unknown quark masses, we obtain similar mass values for both the up and the down quark as follows:
[1] Note, binding energies for both the neutron and proton have been attributed to the ‘gluon’ in the standard model. The gluon would have to possess a mass that is far from negligible. In fact, it is assigned the bulk of the total mass of these baryons. So, to say that the proton and neutron are comprised of up and down quarks is extremely misleading when expressed by advocates of the conventional view. The gluon is assigned by far the largest majority – over 99% – of the total energy of a neutron. In this post we are explaining alternative approaches.

However, in an alternative decomposition of subatomic particles into constituent quarks, two colliding neutron-like particles break up with the quarks recombining to form a proton and electron. For this decomposition one obtains:
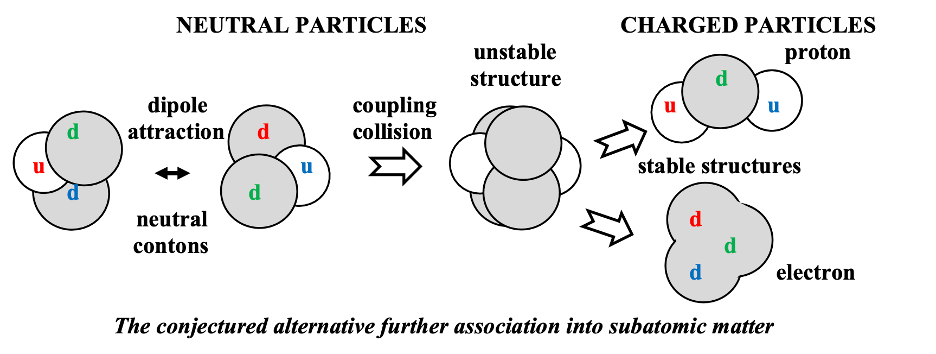
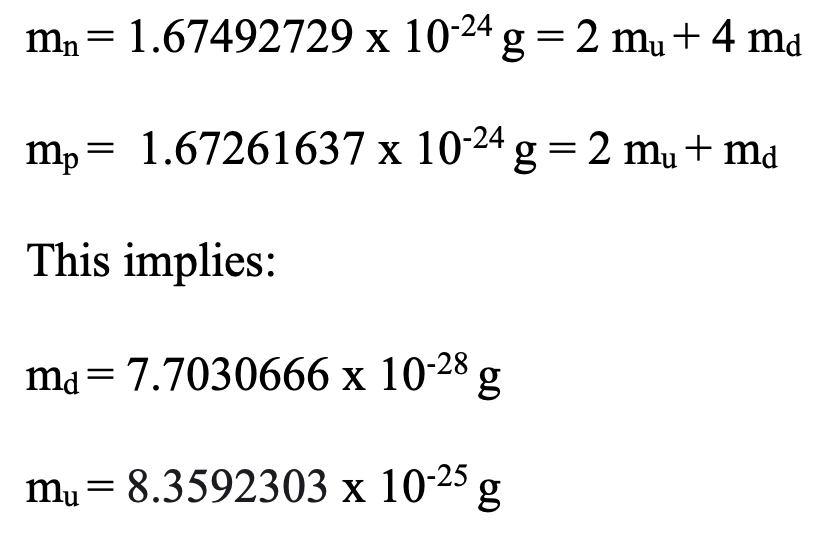
But assuming the electron subsumes the three extra down quarks, there is an additional constraint. As demonstrated for Poisson charge distributions in other papers discussing neoclassical field theoretic topics on this site, when multiple fundamental charge distributions are concentrically superimposed as are the down quarks in the electron decomposition, the result is a single distribution with n-squared times the self-energy of just one of the n distributions. Thus, in the case of the electron with n=3, we posit m_d = m_e ⁄ 9.

Then we must re-do the mass estimate based on the neutron and proton mass equations, noting a difference of 0.005 x 10^-25 g between them, so we take the average:
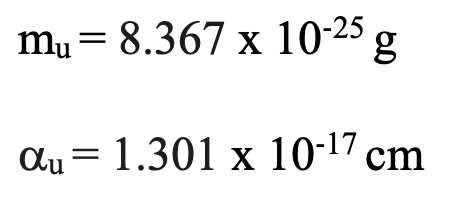
The slight difference in the mass estimates of the up quark from the two sources (proton and neutron) is easily accounted. It is due to the different numbers of each type of quark with their associated binding energy differences in the corresponding host structures. But the implied differences in the exponential variance of the up quark is minimal.
All of this is just preliminary grocery shopping for use in upcoming recipes for a ‘quark soup.’
Leave a Reply