Investigations into the generally observed invariance of the spectra of electromagnetic radiation after having propagated to a considerable distance from its source through a scattering medium by Wolf and others led to the discovery of an associated general scaling law. That law specifies the conditions under which this traditionally-assumed cornerstone of spectroscopy remains valid. of interest is whether this law precludes forward scattering through intergalactic plasma gases from altering the wavelength of light propagated through it? It has been accepted as ‘fact’ that it doesn’t. We will show, however, that under certain conditions realized in hot plasma gases, it does.
Wolf found that single-scattered emanations used in his investigations that violated this law could not support forward scattering through multiple extinctions that is essential to undistorted image viewing. In those cases, the degree of alteration of the spectra was produced by the introduction of a commensurably appreciable scattering angle. This conclusion was essentially that promulgated by Zel d’vich in his precipitous denial of even the possibility of any ‘tired light’ model of cosmological redshift. These results and their implications bear consideration with regard to conclusions we will obtain farther on when we see that there is an angular convergence rather than a divergence of forward-scattered radiation in a relativistic thermal medium. That repeatedly convergent angle is indeed what is associated with cosmological redshift.
But we need to understand the proof of spectral invariance if we are ever to prove that, in fact, there are assumptions made in this proof that are not realized in the intergalactic plasma medium with which we are concerned. Of primary importance in this regard is the fact that it was made very clear that relativistic speeds of the scattering electrons were specifically excluded from the proof. So that’s the direction we are headed.
the proof of the law of spectral invariance from distributed sources
In demonstrating invariance, Wolf showed that if the degree of spectral coherence, mu realized the particular mathematical form throughout a distributed source obeyed the condition:
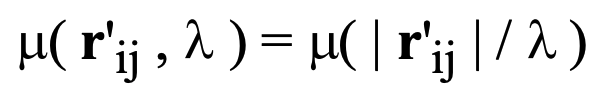
then radiation from that source would remain spectrally invariant.
The expression for ‘spectral intensity’ or ‘spectra’ of radiation is:
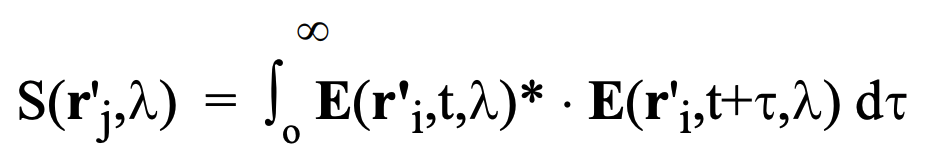
The degree of spectral coherence is obtained as follows:
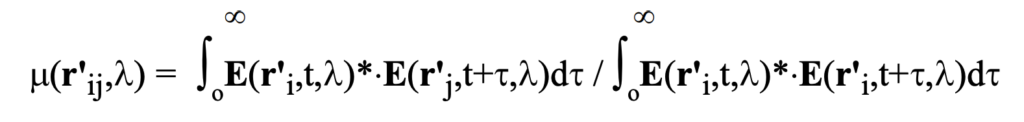
Thus, ultimately Wolf’s law specifies the coherency conditions between electromagnetic fields emanating from the constituents, p_i and p_j of a distributed (secondary) source as illustrated in the
previous figure below.
In the analyses performed by Wolf et al. (1989) of scattering media by analogy with primary distributed sources, they considered only a single extinction/re-radiation process (as in the figure). They also very explicitly excluded consideration of the motions of the individual dipoles; that limitation was adequate to support their results.
This law is compatible with Lambert’s radiation law applicable to blackbody sources and other usually-studied thermal sources, which is a special case of of this law for which:
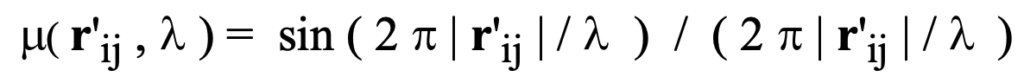
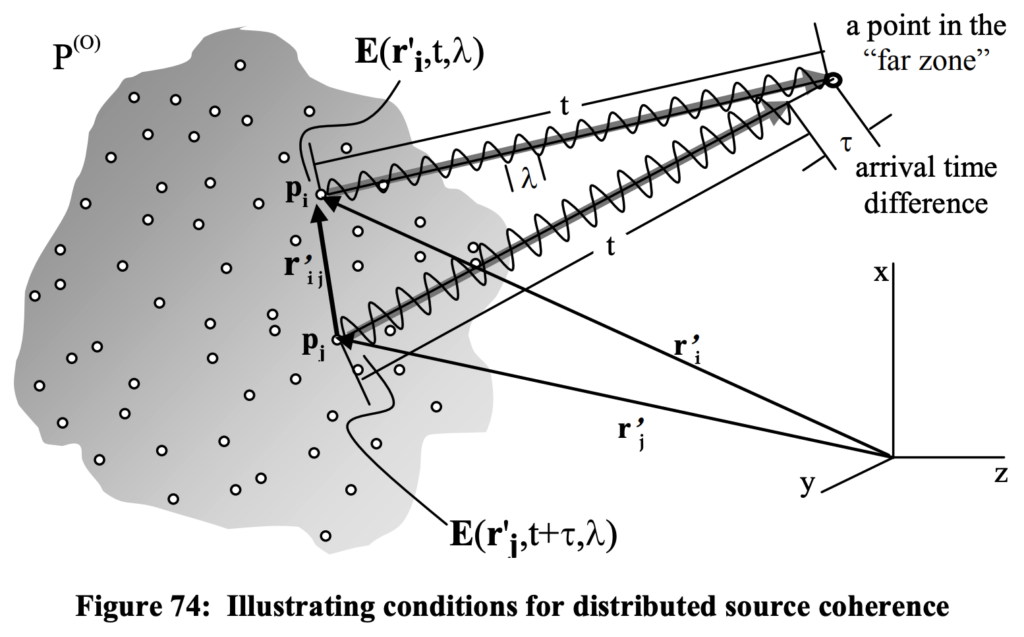
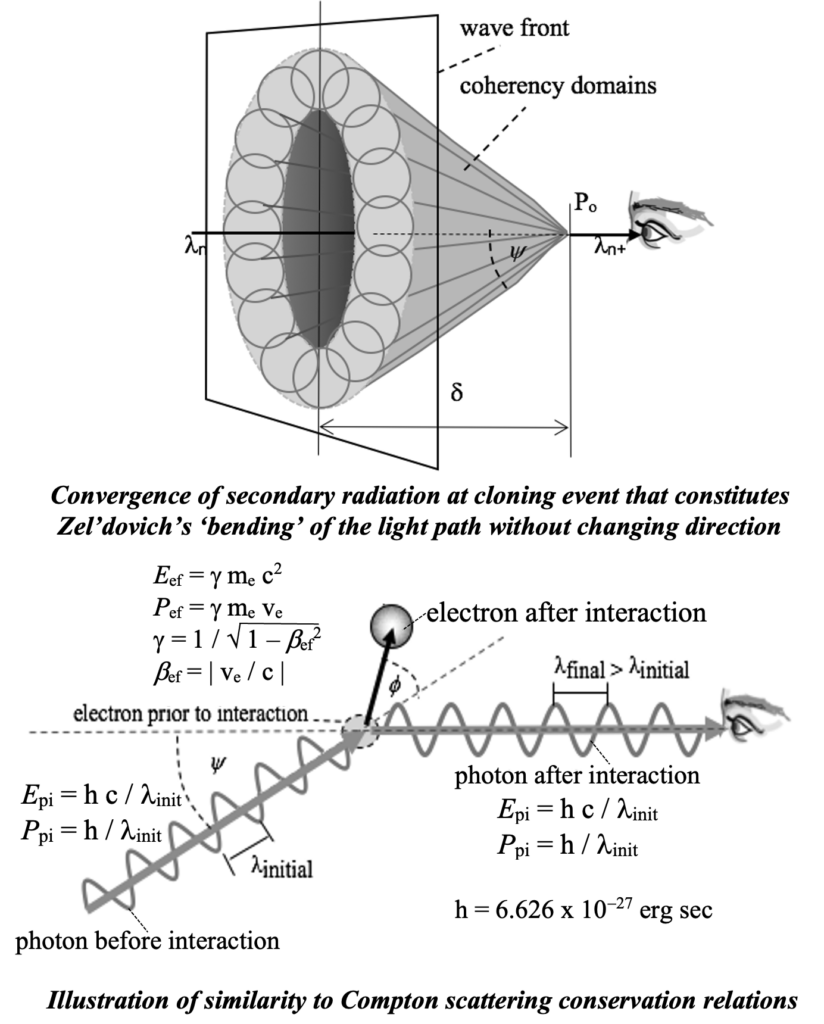
Lets analyze what this says: Wolf pointed out that by distributed source, it doesn’t matter whether the source emitted ‘primary’ or secondary radiation. The property pertains to the coherence of the emitted radiation from the individual component sources within the ensemble. If the individual secondary scattering electrons all emit radiation with common spectral properties, then the recombined radiation that is detected will posses those same properties. It was assumed whatever produced or induced the emission of the radiation was the same in every case. In forward scattering it is assumed that the spectral properties of the common phase of incident radiation is identical for each electron in the coherency domain. At the focus, P_o of each coherency domain there are, over any appreciable region of space many electrons detecting the same radiation from their own unique coherency domain.
The condition indicated by Wolf’s scaling law do not specifically apply to a primary thermal source because of slight (but major relative to the coherency length of photons). The individual Doppler shifts associated with the distinct motions of the constituents, p_i and p_j result in the well known spectral line broadening of thermal source radiation. There is a spectrum of different photons all having slightly different wavelengths. Transverse Doppler shifts also occur, of course, but those will be of second order in beta_i and therefore typically insignificant relative to the radial Doppler effects which will be first order in beta_i, where beta_i = v_i / c and v_i is the velocity of the component p_i.
So what this theorem does not address is the effects of velocity differences of the constituents of the secondary radiation that occur within the coherency domain. All of these secondary emanations are being incorporated by means of coherent interference into the single photon that is being ‘cloned’.
The effects of the radial motions in a secondary source with a zero mean velocity distribution will be reduced to fourth order effects in beta_r and will cancel out in any case after repeated extinctions through the coherency domain because they are equally likely to be red or blue shifted. However, the transverse Doppler effects are second order in beta_i at every extinction and are always red shifted as was shown in the figure in the previous post. Thus, the transverse Doppler effects accumulate without limit. We will pursue this avenue of investigation. It will prove to be extremely significant. Although these transverse Doppler effects are nearly always negligible in any one instance, they are additive and therefore may accumulate to significance. In the case of the extremely large number of extinctions and large free electron velocities that pertain in particular to the intergalactic plasma medium, we will show that they accumulate very significantly, ultimately producing cosmological redshift.
relativistic effects pertinent to forward scattering in a plasma
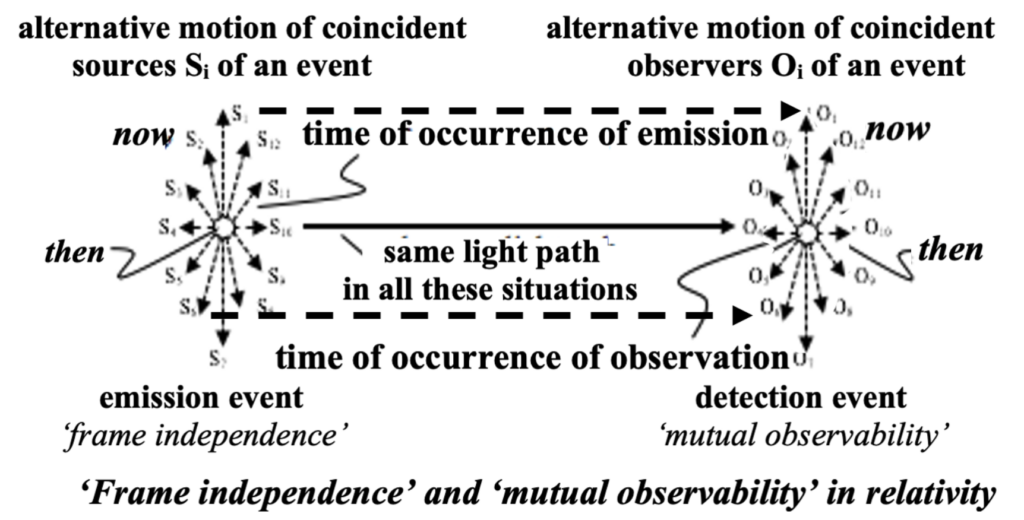
Implicit in Einstein’s theory of special relativity are frames of reference and the Lorentz transformation equations. There is also the concept of ‘frame independence’ that involves the fixing of an event relative to an observer’s frame of reference independent of the velocity (and therefore, the frame of reference) of the object(s) on which that event occurs. Those objects are sources of emitted radiation. Radiation from sources in the neighborhood of a location and time in the event space of an observer that constitute ‘coincidence’ when emission events occur will all appear in the same direction and require the same amount of time to arrive at the observer in his frame of reference. In the figure below, all of the twelve sources plus the one at the center that is stationary with regard to the observer (identified as a detecting electron e) emitted light at the moment they passed through the designated event location. All will be seen as one although with slightly different red or blue shifts.

If each of the twelve sources had been fixed in the frame of reference of an associated observer (electron), the coincident emission event would then be observed by the respective observers at distributed locations and times (observation/detection events) as shown below. They will all detect the radiation from the same direction between coincident events even though they are no longer in coincidence. It is significant that frame independent coincident events cannot be observed by relatively moving observers at the time they are in coincidence. If the detecting electrons were to oscillate in response, the resultant emanations would likely not constructively interfere because of the the disparity in the occurrence times and locations outside of the coherency length of the radiation. Secondary emanations from the respective detecting electrons will not contribute to coherent secondary radiation moving forward.
However, there are huge regions for which plane waves approximate the spherical wavefronts from distant primary sources of radiation. The radius R of the central Fresnel zone throughout which plane waves apply is the following:

For visible light from cosmological objects this radius would be on the order of ten thousand miles. All electrons on each of the planes experience in-phase incident radiation, when they emit induced radiation in the frame of reference of a detecting electron will be coherent with the similar induced radiation from a different region on the plane that is in the same direction for a differently moving electron. And when they detect this radiation when they are in coincidence, their induced radiations will be coherent.
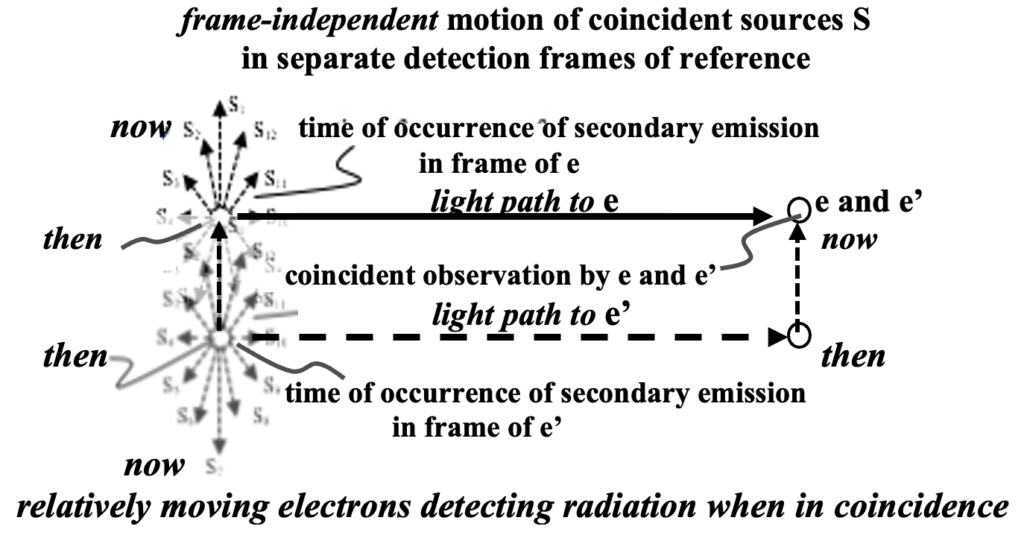
Clearly, if e’ were detecting the source that is relatively stationary with respect to e, then the light path and travel time would be longer by the gamma factor — which could be as much as years. So every electron that emits secondary radiation to contribute to the ongoing forward scattered radiation derived their contribution from a completely separate group of preceding electrons.
The scattering from electrons at or near a plane of common phase of the incident radiation involves a transition of electrons entering, to those leaving, an area of approximate coincidence where secondary emission takes place. The area from which light is detected will depend upon the velocity of the detecting electron, but the secondary emissions from all electrons will proceed in the same direction at the next step in the propagation process.

Thus, relativistic phenomena significantly alter the coherency domains that are essential to the photon cloning process. The very concept of relative motion assures us that whether the velocity is considered that of an emitting or of a detecting electron is immaterial. But the coherency domain is associated with observation and therefore belongs in the frame of the detecting electron. So an electron moving parallel to an incident constant phase plane will detect both scattered and incident light from the closest region on the phase plane at the time it was emitted, not from the same region on that plane as other relatively moving electrons, so time dilation is not involved. This is aspect of the phenomena is not the result of relativistic aberration; it is from the opposite direction. It applies to secondary radiation from distinctly unique electrons as shown below:
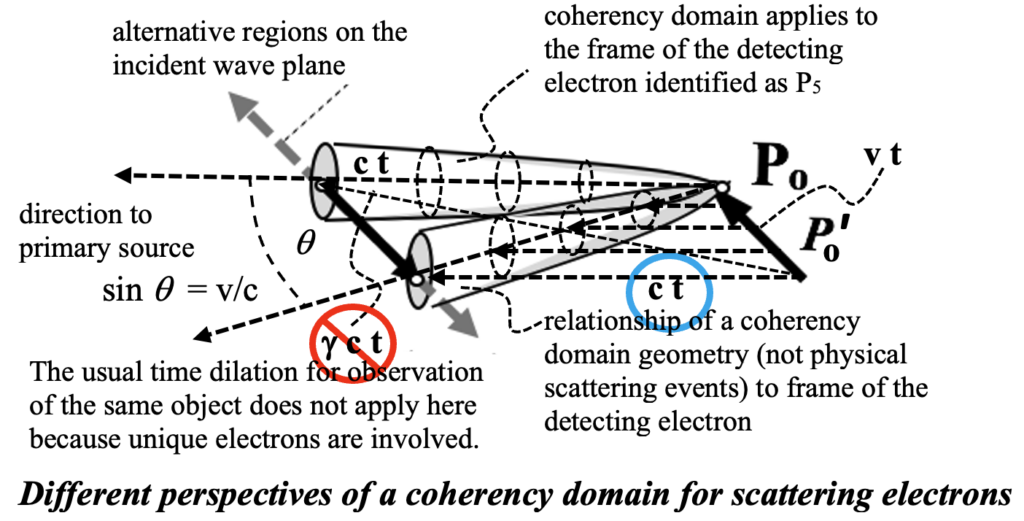
The relativistic process is spread out into a penumbra of coordinated coherency domains, whose angular spread is proportional to the velocities of the scattering electrons. It is the velocity of the detecting electrons that affect the angle of associated coherency domains, and the determination of electron velocity distribution is a thermodynamic issue. The distribution peaks around a mean and so the angullar spread of domains will be similarly spread as shown in the next figure.
There is a convergence of scattered wave functions associated with the photon such that Zel’dovich is both correct and incorrect as far as his assessment of scattering in an intergalactic plasma medium. There is a momentum exchange and there is a bending of each light path, but because it is convergent rather than divergent, there is no net change in direction. The conservation laws to which Zel’dovich deferred are essentially those that pertain to the Compton scattering effect of energy and momentum being transferred to electrons.
The electron velocity distribution derives from the Maxwell/Boltzmann distribution of energies for which the average root-mean-squared transverse velocity component is:
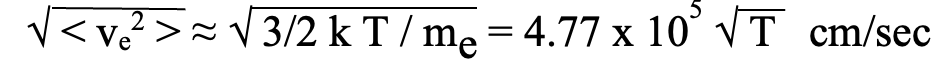
The constant k is Boltzmann’s constant and me is the mass of an electron. This solution is valid for temperatures T to about 108 K, a value sometimes encountered in intra-cluster plasma, this non-relativistic formula provides a fairly accurate approximation up to two or three percent of the speed of light.
It is the angular bending of light paths that transfers energy and momentum to the medium as Zel’dovich averred. So the temperature of the hydrogenous plasma through the coherency domains affects the amount of change in the wavelength through each coherency domain along a light transmission path. Applying the results of Compton’s conservation analysis to a single coherency domain of forward scattering, one obtains the following net change in wavelength per cloning interval:
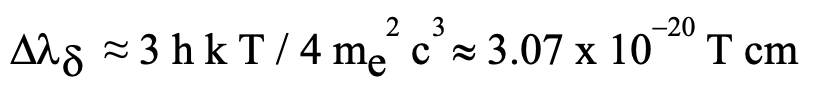
The constant h is Planck’s constant. Thus, wavelength is increased at every cloning interval independent of its original wavelength, but that is not in itself a redshift. The definition of redshift is the accumulated change in wavelength divided by the wavelength from the primary source emission. The net effect on the original wavelength after n extinction intervals can be determined by regression as follows:

As seen in the plots below, this does not provide a redshift-distance relationship per se. To demonstrate the relationship of distance to the change in wavelength the distance r(n) as a function of the number of cloning intervals n must be established. But because the length of these intervals depends upon the wavelength entering the interval, r(n) becomes a summation of the lengths delta(lambda) that are continuously changing rather than just the total number of intervals N times a uniform length. The length of a coherency domain is also dependent on the free electron density as defined earlier,

so the length of the domain will vary as the density changes in passing through a galaxy cluster. Because of the inverse relationship to wavelength, the net result is wavelength dependent with functionality that constitutes redshift. Using formulas derived above for the length of the extinction interval, delta, we obtain.


The curves of r(n) vs. n are plotted for the averaged dynamic pressure of free electrons < Te | rhoe > determined by averaging the product of Te and rhoe at each point along the transmission path. If we plot r(n) vs. log n we obtain the plots below with an asymptotic approach to linearity on a log graph.
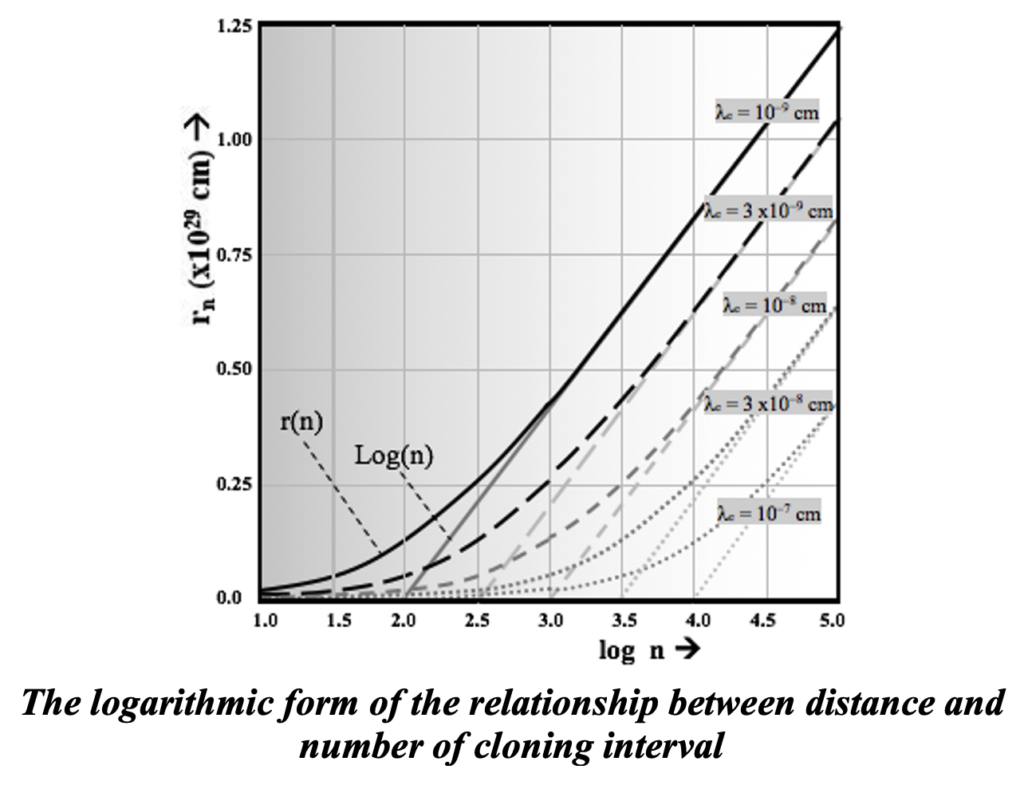
In situations for which merging the functionalities of r(n) and Z (n) is warranted, one obtains a distance-redshift relationship by plotting one versus the other. When one does that, the dependence on number of cloning intervals n is eliminated. Since distance is a linear function of the log of n for large n but inversely dependent on emission wavelength, the distance versus redshift plot is extremely similar for all values of wavelength. It is a virtually identical relationship that holds from hard X-rays (lambdae »10–9 cm) through extremely long wavelength radio signals (lambdae >107 cm). In this way, at shorter distances we obtain a linear recessional-Doppler-like distance-redshift relation directly applicable to this broad range of wavelengths. It can easily be seen that the wavelength dependence is virtually eliminated for wavelengths greater than 10–10 cm. It is also clear that for wavelengths less than 10–9 cm, there is a unique relationship that pertains at every wavelength.
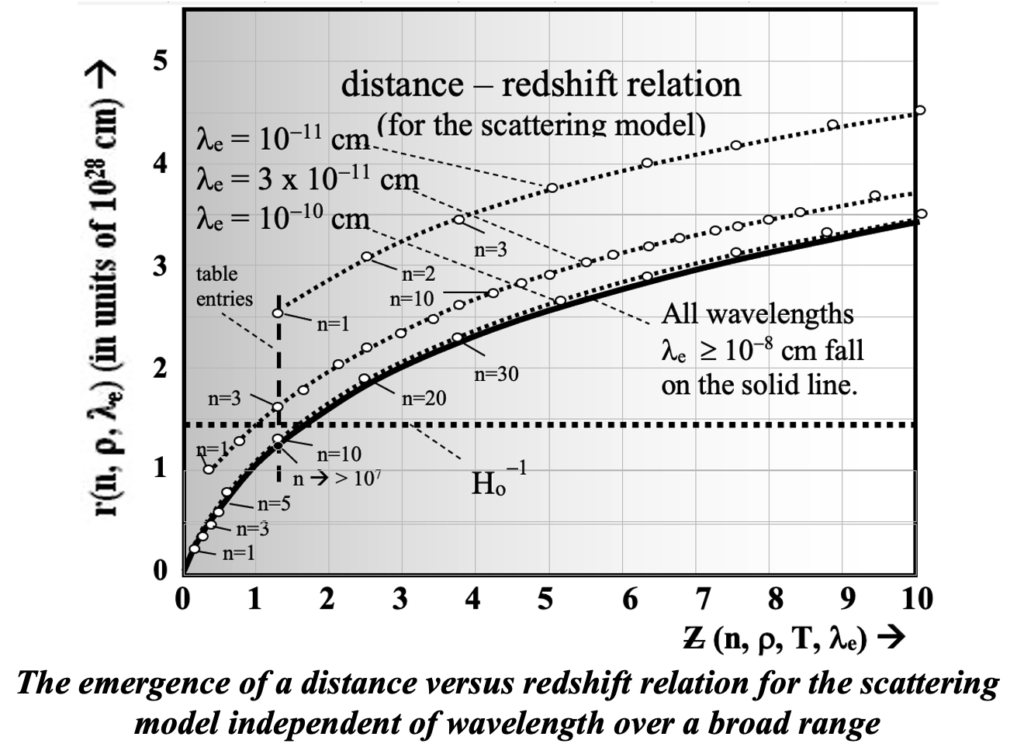
Notice that the numbers of cloning intervals involved in various distances is listed for radiation of wavelengths less than 10^10 cm. For all wavelengths greater than one Angstrom (10^-8 cm), the numbers of cloning intervals is very large for an cosmological distance.
That is the plasma scattering model of cosmological redshift. How it ‘line-of-sight comoving distance’ metric compares with the various mass-dependent versions of the standard model is shown in the next figure.
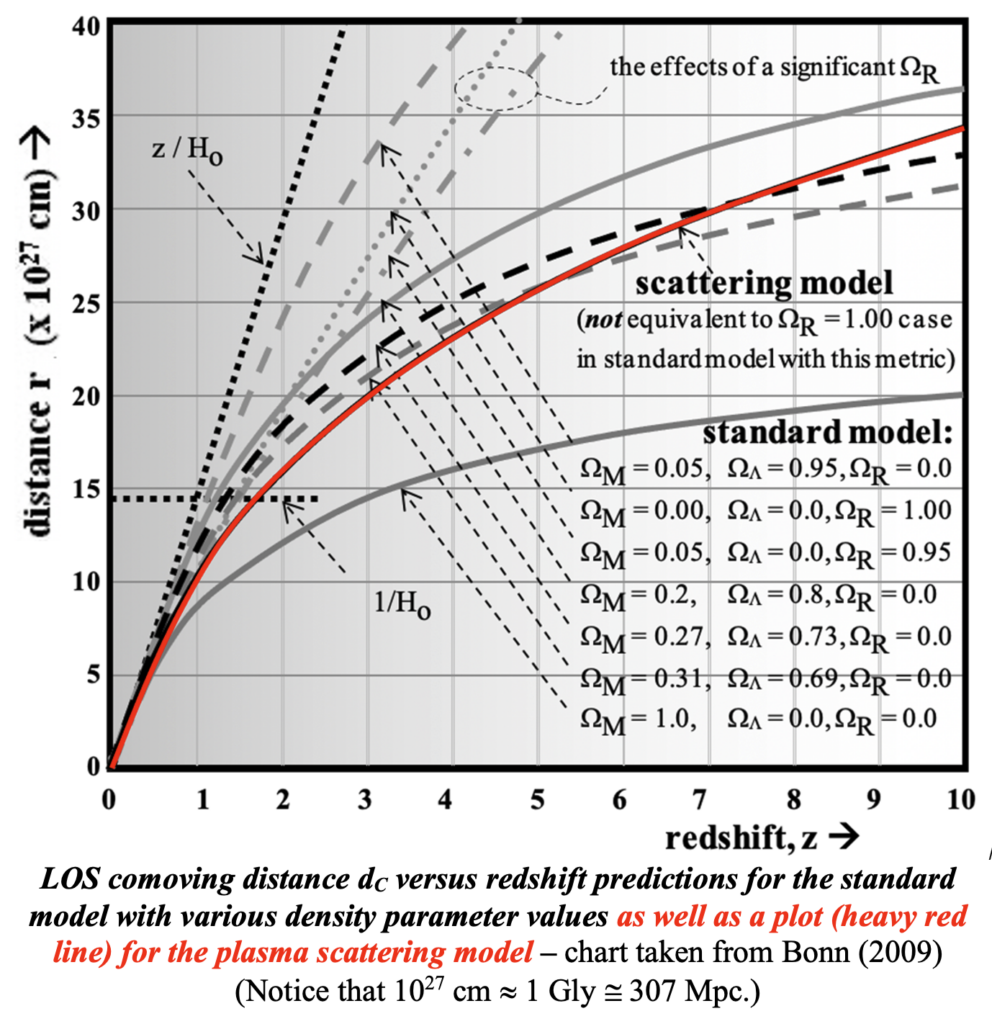
All the ‘distances’ shown in the figures below for the (ΛCDM) consensus version of the standard model involve formulations that include line-of-sight comoving distance. For each there is a counterpart that maps closely for the plasma scattering model shown as the associated darker red lines. There is considerable diversity of distance parameters as functions of redshift in the standard model that can be confusing as suggested by the figure. A consensus on the assignment of a value to Ho and of density values has been a long time coming to obtain a best fit possible to the standard model. Some of the diversity of options of the mass density parameters is illustrated in plots of the previous figure.
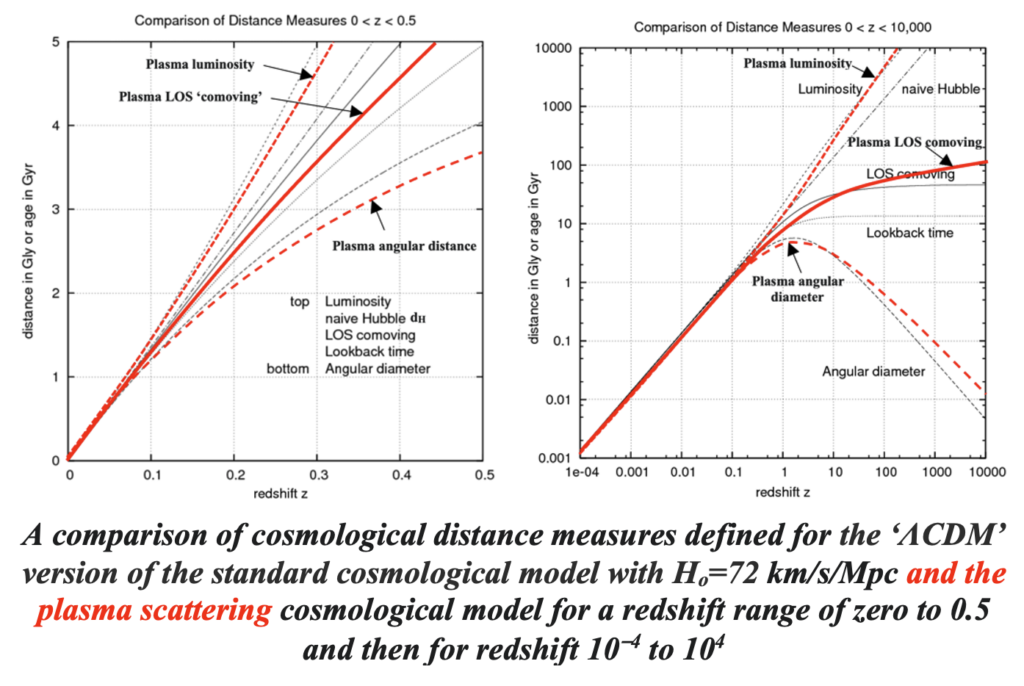
And that as they say, is that.
Leave a Reply