The reader of this and the previous post might well ask, “What does all this have to do with what will actually be observed when incident radiation passes through a scattering medium?” All too frequently that question has been glibly answered in the negative — that there is no difference. To clarify why that is significantly incorrect with regard to the intergalactic plasma, we must understand this processes whereby images of objects are resolved even when they are observed through a scattering medium. So we must understand the process whereby incident photons of radiation are replaced by secondary radiation originating at the scattering electrons.
The mechanism whereby these intermediate scattering electrons effect the replacement of the incident radiation by similar secondary radiation having a different phase was suggested by figure 35 in the previous post. The operative replacement mechanism preserves resolution of images of distant objects so that is not what is at issue. The process involves the summation of the individual effects from a host of electromagnetic fields originating at the intermediate electrons which ultimately overwhelm and replace the incident radiation.
Consider the electric field emanations from the induced electron oscillations of the individual electrons in the scattering medium. The radial components of these electric and magnetic fields diminish as the inverse square of the distance from each electron. This radial component will, therefore, be negligible after a modest distance from the electron. This is in contradistinction to a transverse component of the induced fields, that diminishes as only the inverse first power of distance. This component of scattered electric fields radiates outward as transverse radiation from the accelerated electron. The fields in this secondary radiation will be oriented in the opposite direction (i. e., out of phase) from the incident radiation fields that induced it. The radiation from such a dipole of moment P_e is:
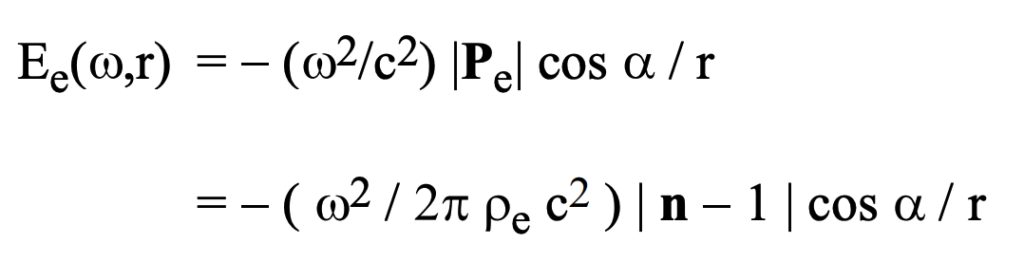
It is assumed that r >> lambda, where r is the distance from the electronic charge and lambda = 2 pi c / w. The angle alpha is the scattering angle of the radiation with respect to the direction of the incident radiation.
With substitution of parameters for the general expression of the index of refraction, the intensity of the radiation will be:

The scattering angle will always be extremely close to alpha = 0 for coherent forward scattering as we will show. These considerations ultimately dictate that there will be cancellation of all fields arriving from outside an angular domain associated with the central fresnel zone that, due to the distances between scattering electrons in the intergalactic medium, will be extremely narrow so that we can assume cos alpha = 1.
coherent radiation from separate scattering events
If radiation from separated sources is to interfere, the oscillating wave functions from each source must be similarly polarized and pass the same observation point within the coherence length of individual wave functions. The coherence length is the effective linear dimension of a photon; it is on the order of 10^7 times the radiation wavelength. (I’m going to be accused of being naive here, but sometimes naivety provides the most intuitive understanding of complex phenomena.) For clarification of coherence length of photons, consider it the number n of waves of a given wavelength that reduces the uncertainty in photon energy to the line width emitted and absorbed by atoms. as shown below.
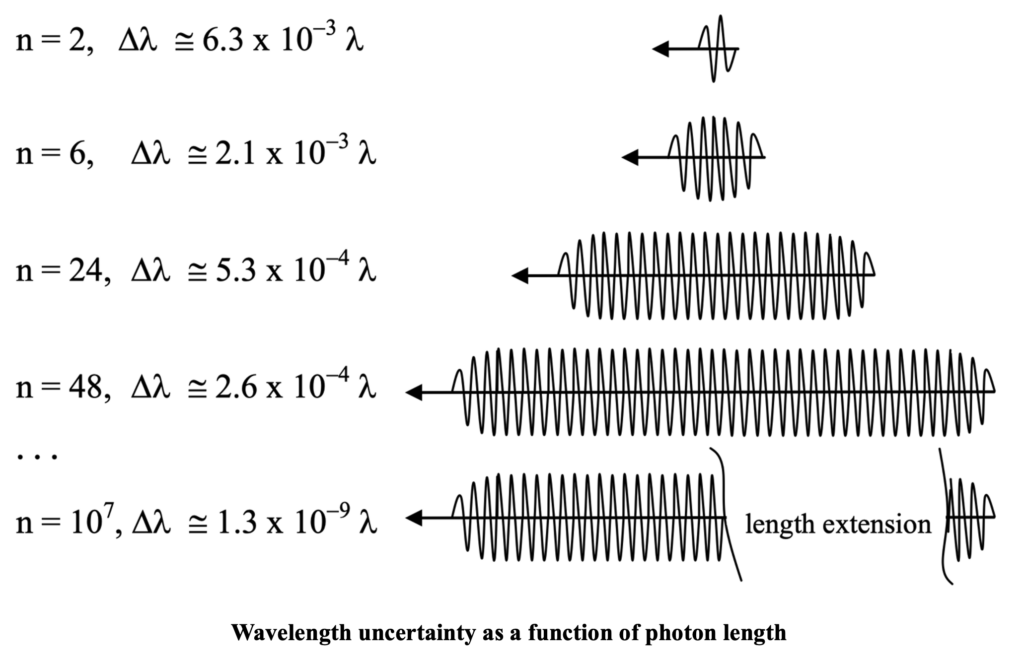
For separations along the light path of photons that are larger than this amount, an entire photon of radiation from one source will have passed the given location before the other arrives. In that case neither positive nor negative interference phenomena will occur. In that case the intensity of radiation at the location will just be the simple result of the accumulation of separate photons from the two sources over a designated period of time.
In figure 70, r_i and r_j represent the distances of two scattering electrons e_i and e_j from the observation location Po. Here we illustrate the situation for which the scattered wave functions from two such electrons interfere. In this case, the scattering phenomena are precipitated by oscillations caused by the simultaneous in-phase arrival of the incident radiation. Let the angle between the two electrons from the perspective of P_o be alpha, with t and t+tau the respective times of arrival at P_o for the scattered radiation from the two electrons. The following implications result from the geometrical relations:
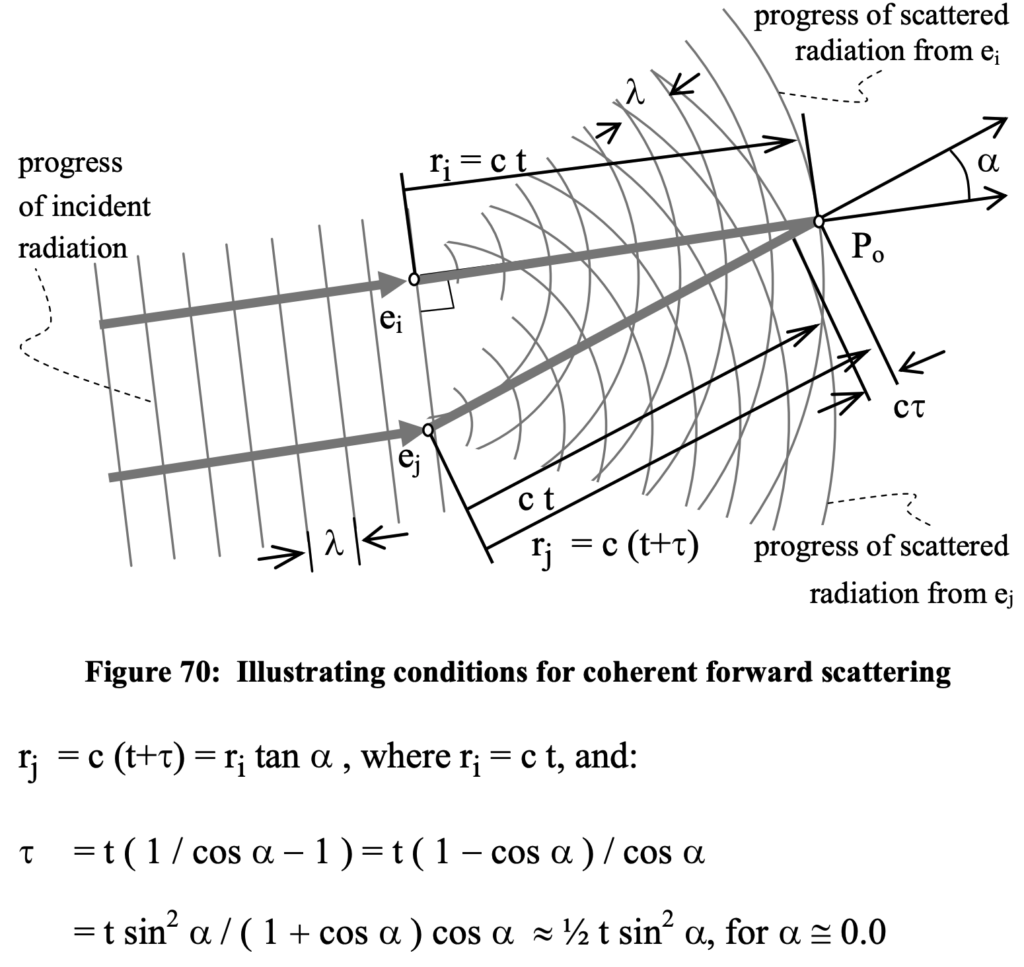
With wave phenomena the phase of the waves originating at separate sources affects the net field strength realized at a given location. So, whenever the value of c tau is an integral multiple of lambda, the two waves will constructively (additively) interfere. This constraint affects the required separation between two electrons if they are to constructively interfere. These constraints ultimately determine the collaborative affect of an ensemble of intermediate scattering electrons on the radiation observed at a given location. Fenn et al. (2000) describe use of this effect in phased array radar antenna systems driven off a common feed. Consider, for example, the scattered electric fields from the two electrons situated such that they both begin to experience the effects of the incident plane wave radiation at the very same instant as shown in figure 70. If alpha is approximately 0.0, as we are positing initially, and will confirm as a necessary consequence, then at P_o a distance c t from the electron e_i we will have for the total field strength of the scattered radiation at P_o:
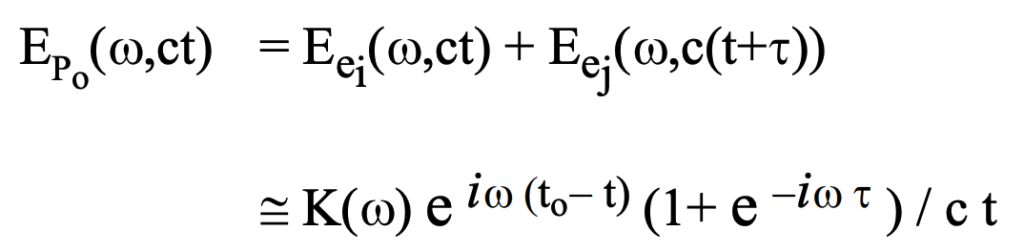
where c t is the perpendicular distance to the plane of constant phase of the incident radiation and K(w) includes all those factors in E_e(w,r) above that exhibit approximately equal values as long as alpha approximately 0.0:
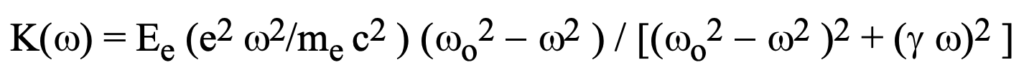
Even at large distances with the constraint of a phase difference, tau << t, appreciable effects result. The instantaneous illumination intensity of this net scattering radiation at P_o becomes a sinusoidal function of whatever that location-dependent phase difference happens to be:
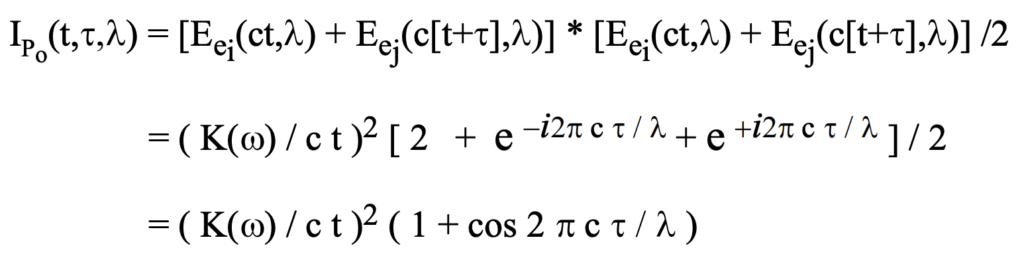
In terms of angular separation of the two electrons from the perspective at P_o this becomes the following as shown in figure 71.
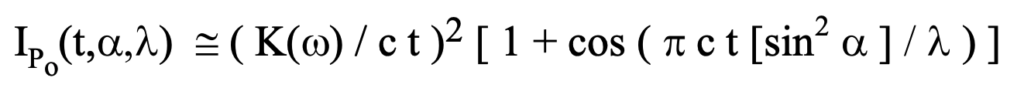
where the general form of the index of refraction is used.
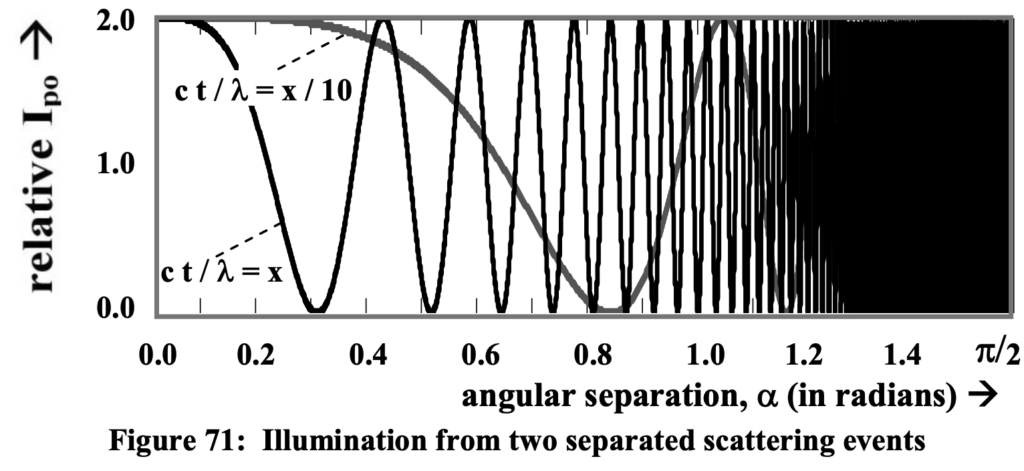
The final term of the trailing factor of the resulting illumination, I_P_o is affected by the relative wave phase, tau of the two induced wave functions. Depending upon the angular separation of the two electrons, the resultant effective intensity of the scattering field at P_o will vary between the extremes of zero and twice the intensity of a single scattering electron as shown. As the distance increases, in addition to the inverse square impact, the predominant central illumination will be narrowed. At appreciable distances it will be very narrow indeed.
Furthermore, rather than just two individual secondary sources interfering, we must consider electrons throughout the entire areas on the planes of incident radiation. Clearly scattered radiation from those electrons closest to the point P_o will constructively interfere whereas radiation from electrons that are further away will increasingly interfere destructively as well as constructively and therefore not contribute significantly to overall intensity at P_o. In figure 72, an annulus of the medium is identified in the thin vertical planar sheet whose thickness is assumed to be much less than the wavelength of the radiation, lambda. Throughout the indefinitely-extended sheet incident radiation is assumed to arrive simultaneously from the left instigating scattering by imbedded
electrons.

Notice that the annulus corresponds to points near an x,y plane that are all approximately equidistant from P_o. Successive annuli of synchronized scattering emanations from embedded electrons whose distances from Po incrementally increase by ½ lambda will alternate between interfering positively and negatively with regard to radiation coming from electrons at the center. The distance for each such annulus can be represented as, r_n = z + ½ n lambda. These zones are effectively fresnel zones. The radii rho_i of each annulus measured from the center satisfies:
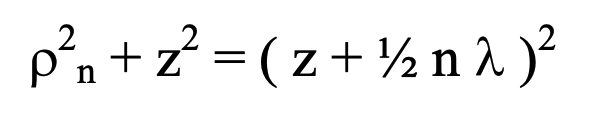
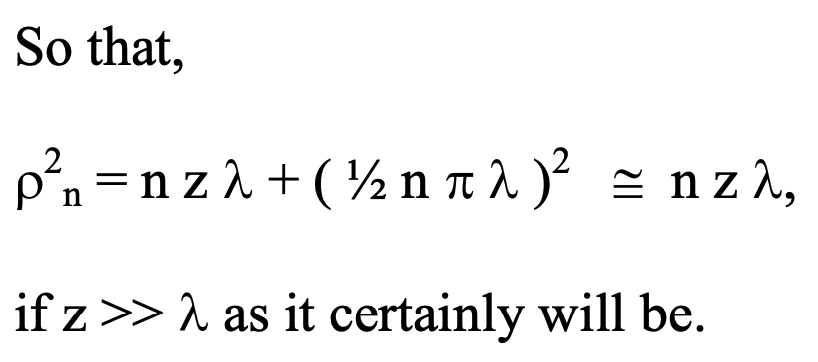
Then if we consider the area within each zone, we obtain:

So that the area of each zone is the same as for any other and, therefore, the intensity contributions from each zone will be the same even though they are increasingly narrower as increases with wave phase.
Since the phase varies even within each ‘half-period zone’, the resultant field strength from each is 2/pi what it would be if the phase were the same throughout the zone. The phase of the
contributions of successive annular zones alternate with amplitude slowly decreasing as alpha increases, so that there is a series which, when added together, sums to 1/pi times the effect that would result from only the first zone if the phase were to have been identical throughout. Thus, by using this factor, we need only include in our analyses the first zone for which,
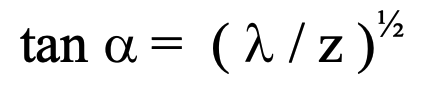
This procedure greatly simplifies integrating the effects of scattering. We have yet to address a means to simplify linear integration all the way from the source to the point of observation. We do that now.
concept of ‘extinction’ in a scattering medium
Statements of what is called the extinction theorem (Born and Wolf, 1980; Wolf, 1971, etc.) all aver that in an extensive medium, the incident radiation will be totally replaced by forward scattered radiation after having propagated to a distance within the medium, delta_o, known as the ‘extinction interval’ that was mentioned in our previous post. This distance at sea level in our atmosphere, for example, is on the order of only a millimeter or so. In the intergalactic medium, in accordance with the sparse electron density of this medium as presented earlier, it can be many thousands of light years.
Throughout any scattering medium, in any case, the radiating fields are continually being replaced. The question is, how long and how far does that process require? Replacement fields, following a first replacement, will propagate at the velocity dictated by the index of refraction, n, of the medium which thereafter completely characterizes propagation through the medium.
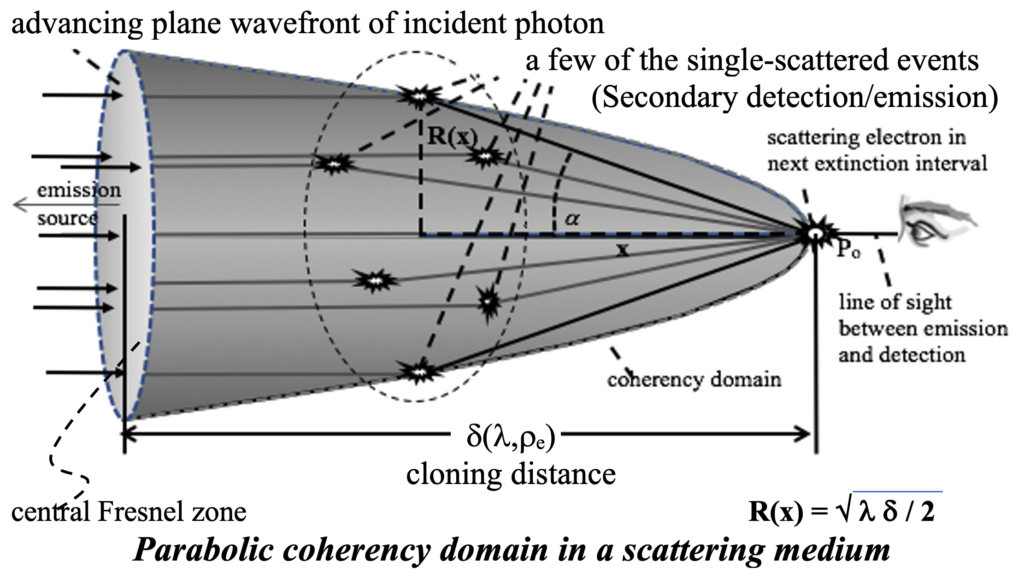
The extinction distance, delta_o, is the distance through a medium, after which incident radiation is replaced by forward-scattered radiation. We define a volume enclosed by a conceptual horn of length delta_o shown in the figure below that we will refer to as the ‘coherency domain’ of the point P_o. Scattered radiation emanating from charges within the surface of this horn define the limits the integration that determines a total forward-scattered field E_net(r) at P_o, thus effecting the incident wave extinction process. The horn is defined as being elongated just enough so that there will be replacement of the incident field by the similar forward scattered field, which is out of phase with it at the point, P_o.
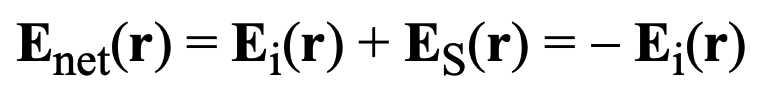
To effect eventual replacement of the incident radiation, the scattering field must eventually overpower the incident field, E_i(r):

where E_S(r) is the resultant of scattered fields derived earlier. It is:
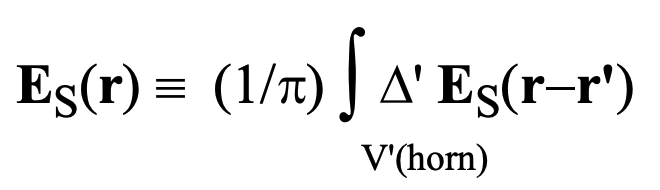
where r is evaluated at P_o and r’ specifies the position of electrons within the infinitesimal volume of integration denoted in figure 72 as DeltaV’. By substitutions like those performed for individual electrons above, a scattered electric field strength, Delta’ E_S(r–r’) can be obtained for each infinitesimal segment of volume in the coherency horn as follows:

The net scattered field at any point within the medium can then be obtained as the integral all these infinitesimal fields. The dimensions of this coherency domain is wavelength dependent as shown in the next figure

Every scattering electron is associated with a coherency domain that determines its secondary radiation as shown below:
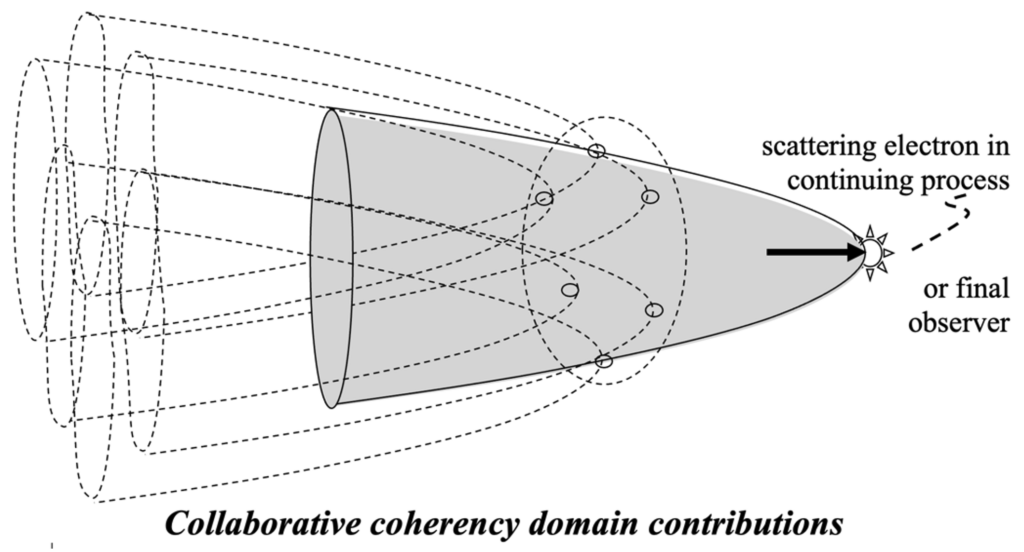
integrating coherent scattering effects
Clearly the net effect of incident radiation includes the contributions of due to polarization of the medium (scattered electromagnetic fields induced by the incident radiation) resulting from all intermediate electrons in the medium. This contribution is determined in large part by phase considerations of the various components received from each scattering electron throughout the medium as discussed above. Ultimately coherent reinforcement of all of the various forward-scattered fields over the total volume of integration results in sufficient scattered field intensity to effect the replacement (or what is called extinction) of the incident radiation by the virtually identical scattered fields that have an opposing phase.
Geometrical considerations are employed to simplify considerations whereby the angular bounds of integration can be reduced to include only the first half-period zone as discussed above. Importantly, although the result of the integration we will obtain is well known, understanding the constraints of integration illustrated in these figures is key to understanding the alterations that will be required to accommodate for the similar, although significantly different, process in a hot plasma in our next post.
By restricting the angle, one can proceed using only the first fresnel zone as if all scattered radiation from within this angle shares a common phase. Thus the overall range of integration will be greatly reduced by the allowed angular restriction identified above as alpha = tan^-1 [ pi lambda ]^½. Similarly, the length over which integration must take place need only extend from zero to the extinction distance of the medium, delta_o rather than the all the way to the source of the incident radiation. So that an integration, which must take into account entire planes of synchronized scattering events induced by incident plane wave radiation and further extended to include planes from the point where evaluation takes place to the source of the radiation, is greatly simplified. The envisioned integration procedure obtains an accurate value for net electromagnetic scattering fields experienced at any point P_o.
We will perform this integration here to determine an extinction distance for the intergalactic medium, which is essential to determining the cosmological effects of scattering.
determining the extinction distance and base angle
Having established simplifying limits of integration appropriate for the horn illustrated in figures 72 and subsequent figures, with delta_o defining the extinction distance at which total extinction is
accomplished and alpha_o the angular limit at the distance delta_o, we will proceed by instantiating the parameters of integration defined in figure 72, we proceed as follows:

In this way, the accepted average extinction distance formula is obtained appropriate for a plasma (or any other) medium. Clearly, a similar analysis applies to any point within any isotropic homogeneous medium. Brecher (1968) and others have assumed this formula in their analyses of extinction in intra- and near-extra-galactic plasmas. It is certainly reasonable to apply
it to the intergalactic plasma as well.
To assess the value of the derived extinction distance in terms of properties of the intergalactic plasma medium, we must substitute the parametric expression for Re(n-1) obtained earlier. It was:

The former of these alternatives must certainly apply for all radiation of interest, in which case, we have that o as illustrated in figure 40.a in our previous post. Then, applying the
first of these formulas to optical wavelengths (5000 Angstroms) will be used as representative of optical wavelengths as it was earlier in assessing a nominal value of n for this medium) results in:
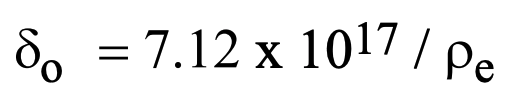
This may be a distance of as much as thousands of light years for visible light with expected values of electron density. It is appreciable by any account, but still on the order of a thousand times less than the distance to our cosmological neighbor Andromeda and many thousands of times more diminutive than distances for which redshift is even considered a marginally reliable indicator of distance.
Notice also that the principal angle at the base of the coherency domain at this distance for optical wavelengths and a plasma density of 10^-6 cm^-3 certainly justifies the assumption that alpha_o is approximately 0.0. It is:
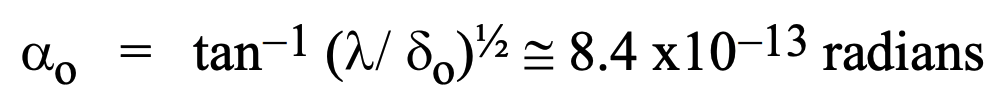
So that for visible light the conceptual coherency domain depicted above would be extremely narrow indeed – even use of the term ‘needle’ would grossly over estimate its breadth. However, because of its extreme length the base may still be on the order of 10^9 cm across, i. e., over five thousand miles. Even background microwave radiation has an extinction distance in excess of a light year or 10^18 cm.
If we look at the total number of scattering electrons N_c involved in the extinction process within a single coherency domain, we must first assess its volume Vc for which we obtain:
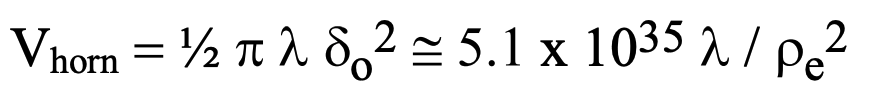
In the case of visible light, the number of electrons involved in effecting extinction in the intergalactic plasma will be:

Despite the low density, this is many orders of magnitude more than are involved in the replacement process in our atmosphere at sea level.
I realize that ten hours of university credit should be offered for reading this post, but it’s a necessary basis for understanding the plasma scattering modl of cosmology which is our objective. However strange the forward scattering processes might seem to those who have not been familiar with them, the replacement of radiation by extinction does not in itself alter the characteristics of the incident radiation. So, since that is the case, why have I drug you through this torture? Because… when we add consideration of the relativistic effects of high velocity on scattering electrons, the resultant radiation emerging from the forward scattering process will have a profound effect on wavelength.
We’ll address those relativistic effects in our next post.
Leave a Reply