Sir Isaac Newton envisioned an infinite universe exempt from gravitational collapsing. Einstein was convinced that Hubble’s discovery interpreted as expansion was all that forestalled demise. His model of an infinite universe was an indefinitely enlarged spherical region of uniform density; he used Poisson’s equation to demonstrate collapse otherwise. That depiction has not been relinquished by cosmologists. A lambda fudge term that Einstein acknowledged as his most egregious error has been requisitioned as the density of supposed dark matter. But they were wrong in their characterization of an infinitely extended universe. Any three-dimensional model of the universe, whether finite or infinite, as an expanded sphere of a given density implies an illogical ‘outside’ of the universe with an outer surface at which any collapse must begin. In such a simplistic characterization, we would be at the center of a non-Copernican universe. Einstein settled on the three-dimensional universe as a surface in four dimensions a shown in figure 1.
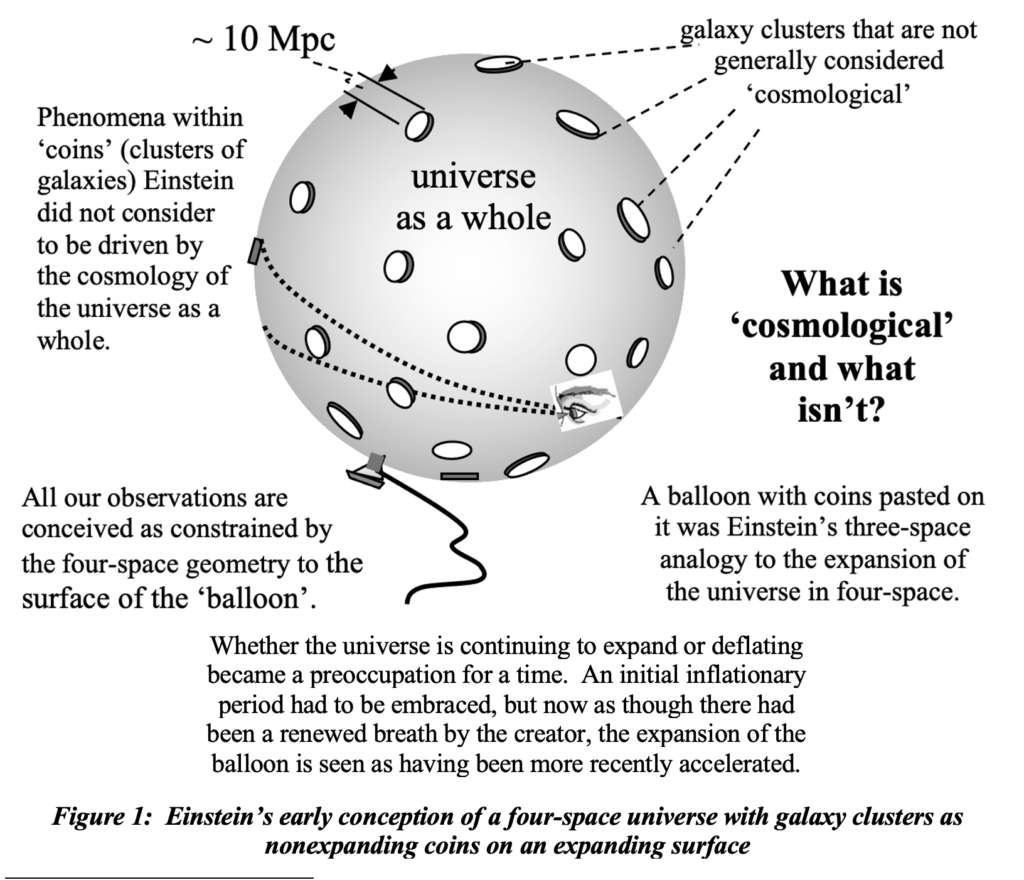
Einstein’s and later also Hawking’s model, not Poisson’s equation, was incorrect. There is no ‘outside’ of an infinite universe. However large the three-dimensional sphere one chooses to represent an infinite universe (refer to the ones on the left in figure 2), there is an equally large sphere adjacent to it, which is still a part of an infinite universe. All the rest of an infinite universe (both inside and outside the larger sphere) is symmetric about that central point of contact of the two smaller spheres, so all gravitational forces cancel at every such point and there would be no collapse.
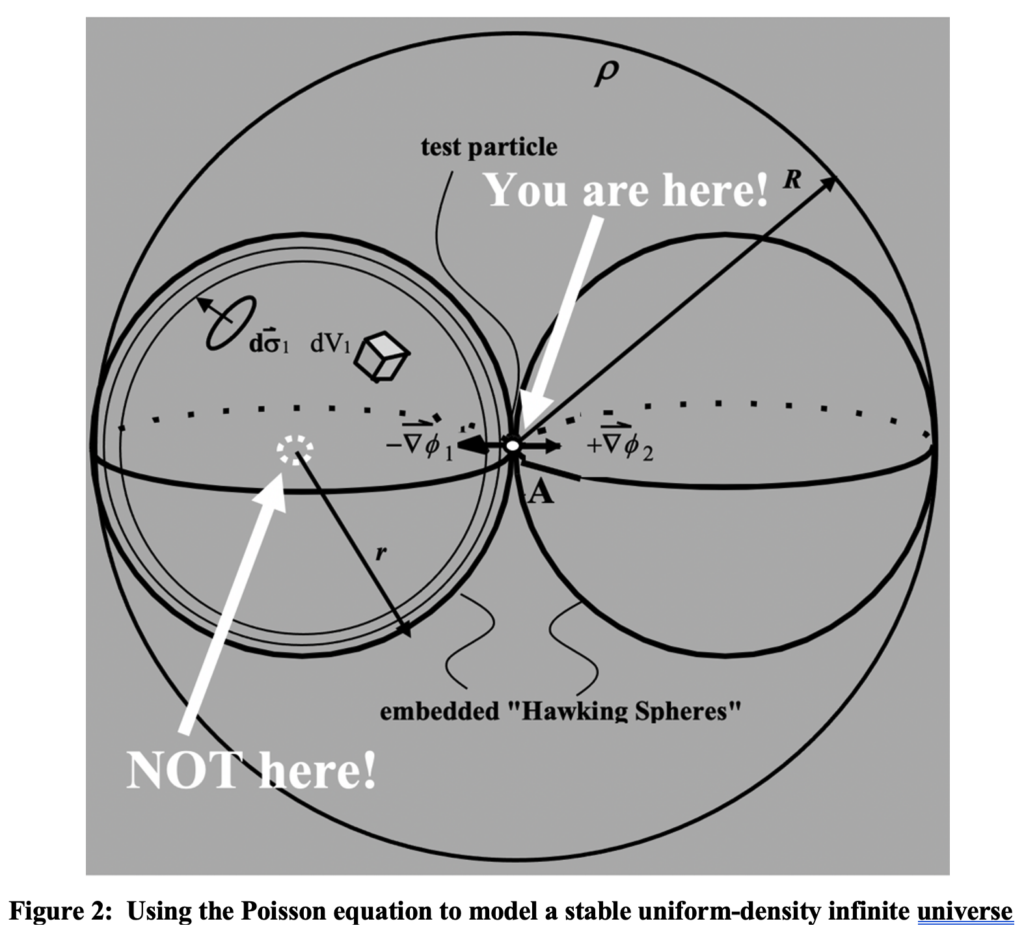
If the left-hand sphere in figure 2 were somehow to have been filled with a higher total density of matter without affecting the surrounding uniform density, it and regions surrounding it would begin to collapse inward forcing a larger and larger exception to uniformity. If instead that sphere was empty without affecting the surrounding uniformity, then the hole would expand indefinitely outward due to outward gravitational force on the particles at the boundary increasing the size of the hole. But if there is a level at which the universe can be considered uniformly dense, the realities of hydrostatic pressure, preclude both these extremes.
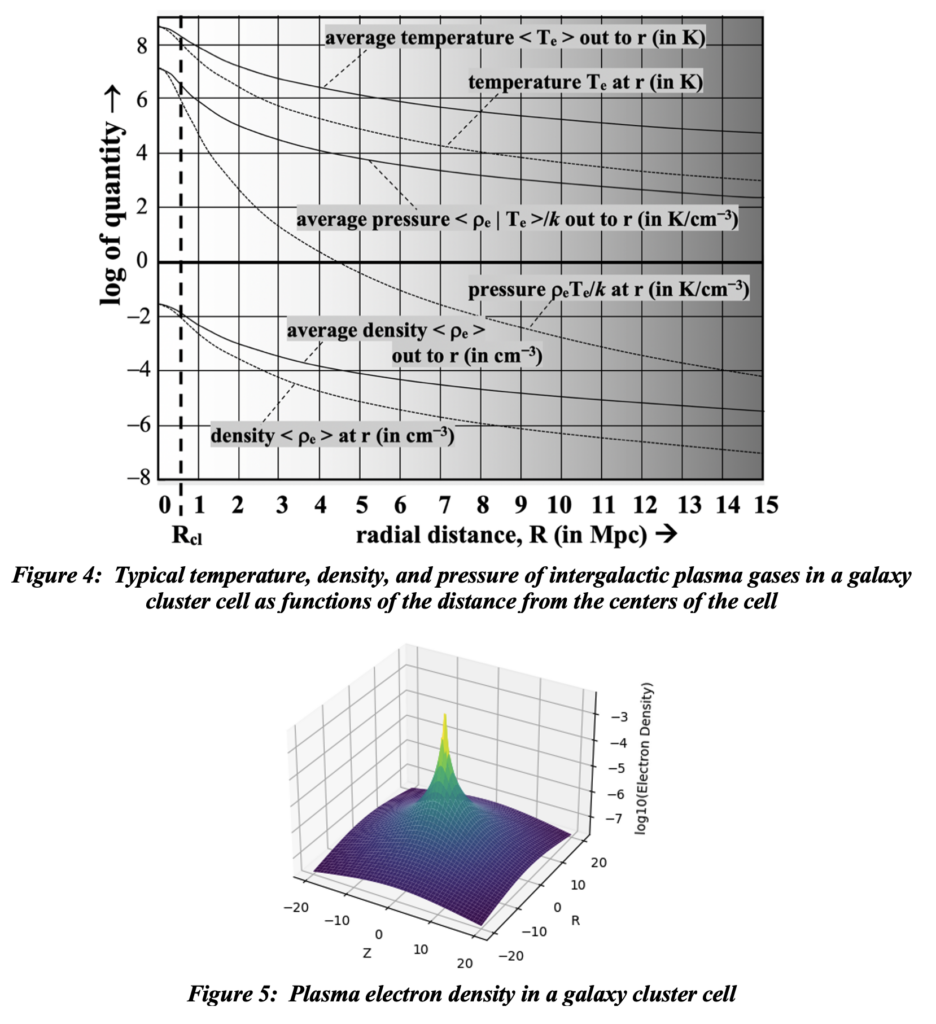
Of course uniformity at the detailed local level of our universe is unrealistic to say the least. Random variations are required of a realistic dynamic model of the universe; that would produce over and under densities in the uniformity. One of the more egregious of Einstein’s errors was in depicting an exclusively gravitational universe. Any adequate model of the universe must include thermodynamic considerations with its ideal gas law for which a stable uniform mass density would be associated with uniform temperature and pressure. Realistic situations of higher temperature and pressure in a denser clump would produce a low-density moat with pressure limiting infalling matter from its outer regions, stability ultimately resulting. A void would be filled in by diffusion due to pressure from the outside until a spherical declivity was filled in enough to counter the outward gravitational force. And unless matter were to have been inserted or extracted from the general uniformity, hydrostatic equilibrium would be maintained with uniformity established at a higher level of granularity. In either of these cases there will be a gravitational clumping toward the center of a left-most spherical region surrounded by a less dense region out to where uniformity is realized at the interface to the sphere where counter forces cancel. This is because all symmetrically organized forces external to the two smaller spherical regions nullify each other. This is shown in figure 3 with typical functionalities of density, temperature, and pressure based on the beta model of galaxy cluster domains shown in figure 4. Variable density regions will expand until average density is reduced to the average uniform density and pressure values, with cancelation of forces at the boundaries with a Voronoi tessellation of space. The averages of temperature and pressure follow mass density at hydrostatic equilibrium as shown.

In over densities temperature as well as mass density, and therefore thermodynamic pressure become orders of magnitude higher than for the universe at large as demonstrated by the plots in figure 4. The electron density of plasma gases that comprise 99.99% of the universe in an over density is shown in figure 5. There is an order of magnitude more baryonic mass in intergalactic plasma than in all the stars of the galaxies that orbit about the center of such an over density. These ‘galaxy clusters’ contain tens, hundreds, even thousands, of orbiting galaxies about a dense central core region as shown in figure 6.
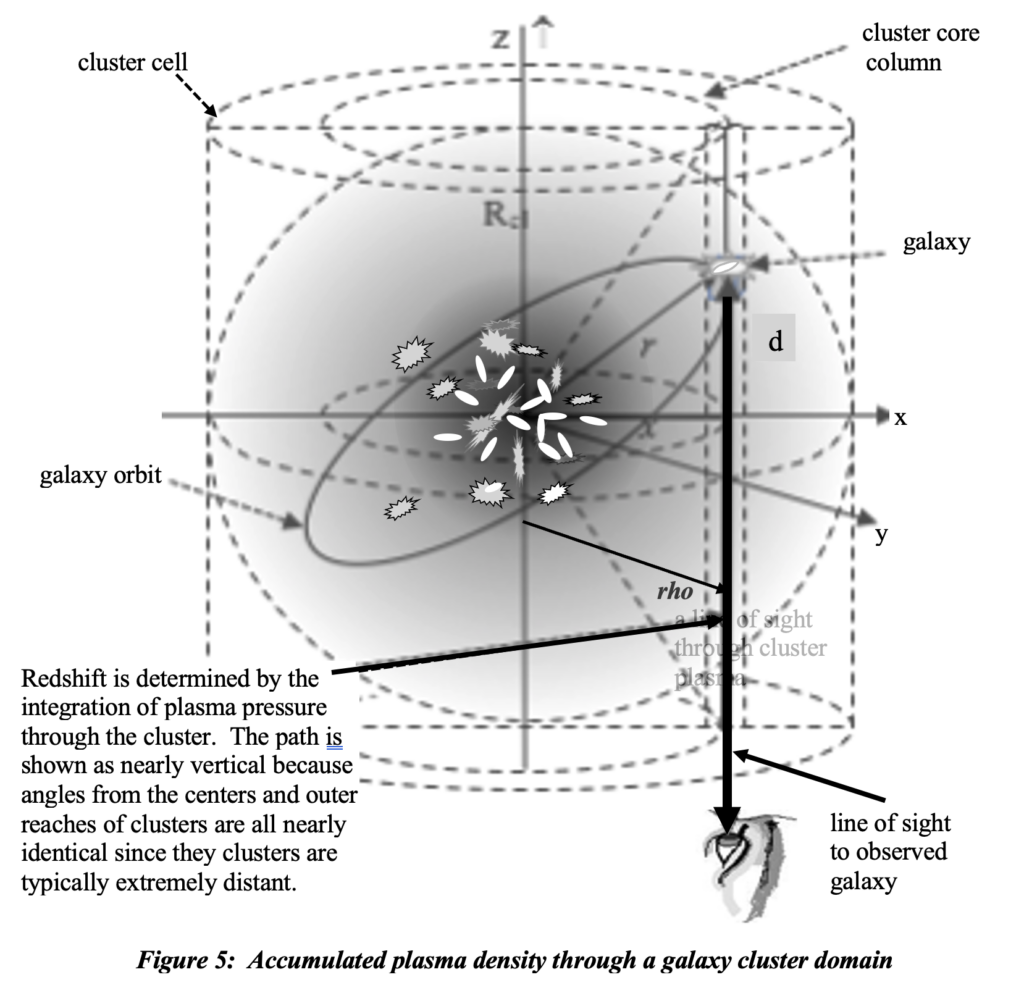
We define a ‘cluster cell’ as the region of space dominated by a single galaxy cluster. This domain is called a ‘dark matter halo’ by cosmologists in deference to mass presumed to be distributed exactly as is baryonic matter although much more massive to effect greater orbital velocities to which they attribute the extreme redshift dispersion through the cluster. The thermodynamic aspect of baryonic matter clustering is not applicable to dark matter, which is conceived as strictly gravitational, incapable of thermodynamic pressures of baryonic matter. Therefore, we consider alternative causes for redshift dispersion in these cluster cells, considering the observable aspects of such domains. Intergalactic gases extend well beyond the typical orbital radii of galaxy orbits near the centers of clusters. The gases are largely comprised of hydrogenous plasma. The centers of clusters are on average separated by thirty to forty Mpc. (An Mpc is a Mega parsec equal to 106 parsecs or 3.26 x 106 light years.) Density and temperature profiles vary with highs in central core regions and values at the midpoint between clusters less than the overall averages of the universe.
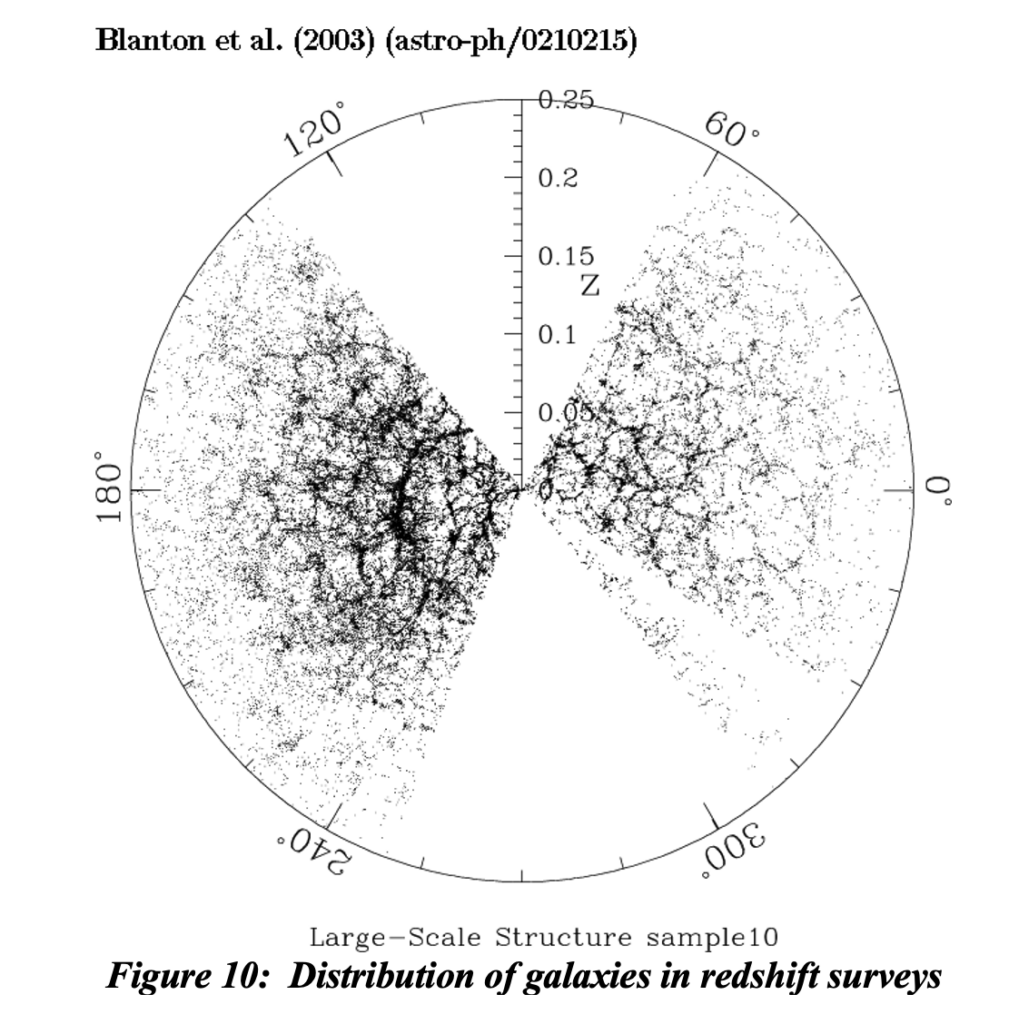
Virgo is a giant, 2000-galaxy ‘super’ cluster that is centered about 20 Mpc away from the Milky Way. It contains some 50 nearby smaller groups of galaxies that suggests that they all form an enormous, flattened cluster of clusters that is called the Local Supercluster. This suggests that there is some higher-level systemic grouping of clusters, which is certainly born out in galaxy surveys. Recent surveys show a clumping of galaxies at distances separated by a redshift of about 0.03 to 0.04 and an associated distance of on the order of 100 Mpc. This apparent ripple effect is obvious in larger surveys that we will discuss relative to figure 10 below.
Space is fully occupied by galaxy clusters; there are zero-force boundaries between them, but there are no complete voids – no expanding empty space. These clusters are not packed together like eggs in egg cartons with space between, piled atop each other for which total volume would be 1.9 times the volume contained in the more spherical regions of cluster cells. They are more compressed distributions of more or less spherical regions with variations in the tessellation of space to be sure. But for representative cluster cells the configuration in column C of figure 6 is what hydrostatic equilibrium produces with representative cluster cells. In figure 7 we illustrate associated force-free boundaries that would occur between clusters in a single layer.

The layers of hexagonally oriented compact structures are fit together in a tesselation of space of dodecahedrons like those shown in the perspective view in figure 8. At large distances the perspective is flattened as we look through increasing layers of clusters; this is illustrated in the tri-layer projection of figure 9. Looking through dodecahedrons comprised of rigid spheres at any angle, no line of sight passes through an empty region – there are no holes through the object. Consequently, after a line of sight penetrates three layers of spherically distributed densities that are extremely dense at the center and sparce at the boundaries, every sparce region is filled with a most dense region indicated by the locations where dark centers fill empty regions in figure 9.
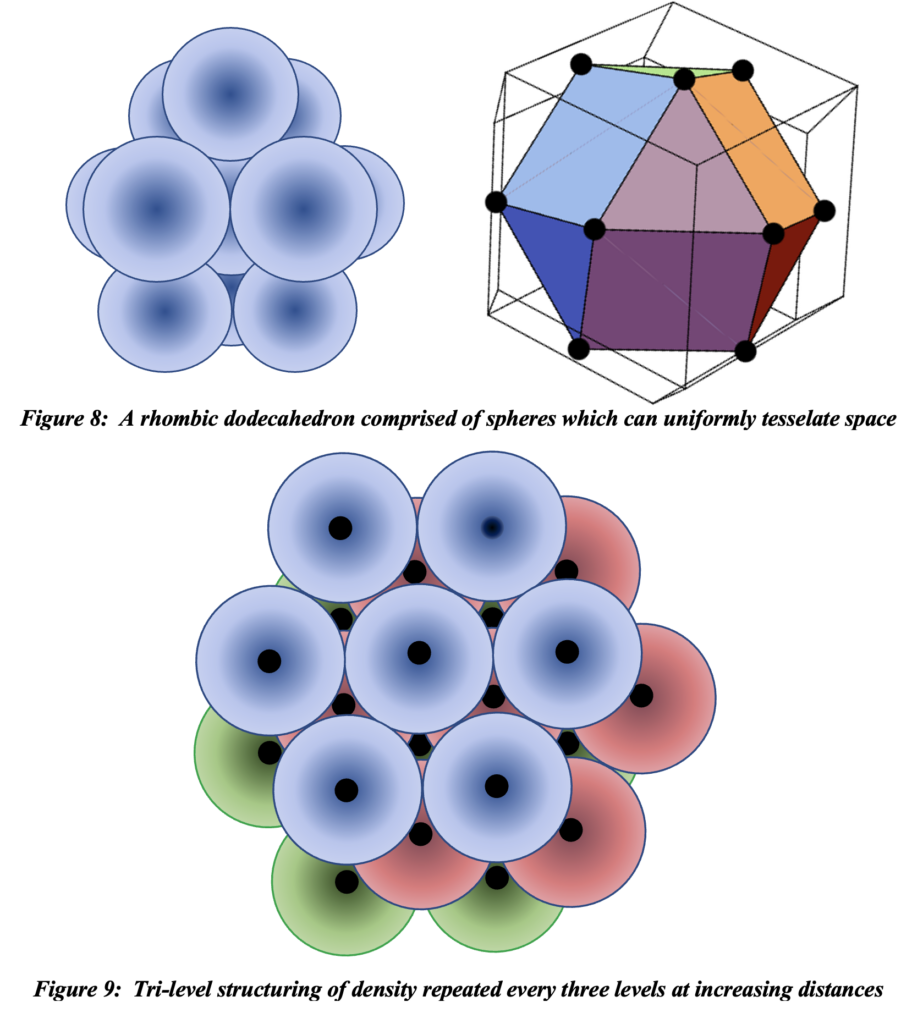
The significance of this fact is that by adding a fourth, fifth, and sixth layer, the density of the same pattern, which will be nearly uniform, will be repeated precisely. With every additional three layers the density will increase by the very same amount and with the same distribution. It is a mere geometrical fact, but when such spheres are shown to be isometric with galaxy clusters, with densities at issue being spatially related redshift contributions, we have accounted for the ripples in galaxy survey data at three times the average galaxy cluster diameter.
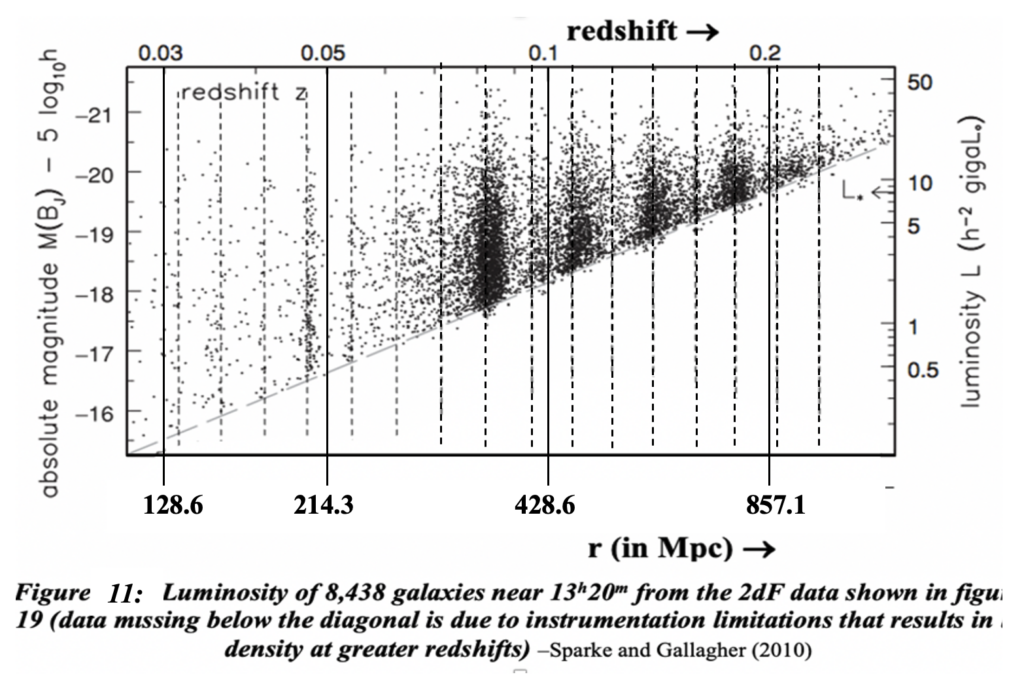
This phenomenon is real. Observations made through layers of galaxy clusters do indeed exhibit periodic ripple effects in galaxy density; these spherical ripples are centered at our location here in the Milky Way galaxy. This is an obvious feature in every galaxy redshift survey like that shown in figure 10. We know that the milky Way is not as a galaxy, any more than our sun is as a star, our earth is as a planet, or Seattle is as a city, the center of the universe. But it sure looks that way. Galaxy survey data can only look that way because of structural aspects that cause it to look as though anyone from anywhere is at the center of the universe. The ripples appear in redshift surveys only because that is the way we measure distance: the periodicity of these ripples is spatial rather than specifically redshift phenomena. See the data presented by Sparke and Gallagher in figure 11 that demonstrates that galaxies appear to occur primarily in concentric shells. The vertical dashed lines are separated by 52 Mpc, so the separation between high galaxy density is 104 Mpc, implying representative galaxy clusters must have a diameter of about 35 Mpc.
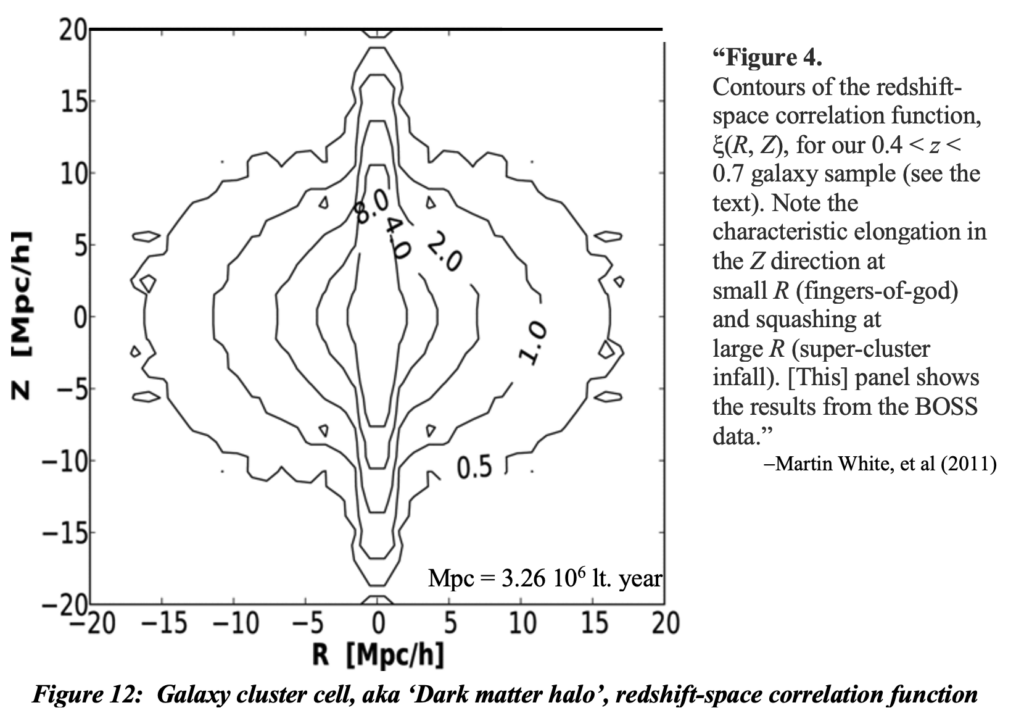
What we have referred to as galaxy cluster cells but more typically been given the name ‘dark matter halos’, tying the ‘finger of God’ effect to its presumed cause. Galaxy cluster cells or domains would have been preferable to ‘halos’ to associate with the ‘fingers of God’ phenomena just to avoid the transference addressed elsewhere. But a rose is a rose is a rose I suppose and by any other name smells as sweet as they say. Research into the nature of the redshift that occurs in light passing through these domains has been addressed by Martin White, et al (2011) under the heading of ‘halo occupation modeling’. It is a fine article that provides excellent data even though certainly not intended for investigating other possible causes of the effects of light transmission through such regions. Figure 12 (what was figure 4 in their paper) provides redshift contribution densities through a cluster as “redshift-space correlation function. That correlation maps directly to the spatial distribution of hydrostatic pressure through the cluster cell. The column density of this quantity through a tri-level space occupancy of cluster cells produces the redshift associated with transmission through 104 Mpc of plasma electrons in the plasma scattering cosmological model, with the lengthening of wavelength increasing redshift increments logarithmically.
The dark circular arcs in figure 10 are not physical like the stone wall of China or Hadrian’s wall. They are artifacts of having to measuring distances to galaxies based on redshift that is dispersed with a three-layer regularity.
If thermodynamic aspects of galaxy cluster cells, including temperature, density, and pressure profiles, had been thoroughly investigated before the cosmology community has acquiesced to the Doppler/dark matter hypothesis, the last century of theoretical cosmology would have proceeded very differently. We would not be re-litigating Genesis. The debunked so-called ‘tired light’ theories of redshift accruing with transmission distance through material substance were disrespected in deference to the well-known recessional Doppler effect. Had the data shown in figure 4 been available, someone would surely have noticed that the redshift effect was proportional to the integral of average hydrostatic pressure as photons pass through the high temperature plasma. It would have been ad hoc at that juncture since a mechanism for such an effect was not yet known. Nor of course was anything known about dark matter –it still isn’t – and yet it was (and is) embraced as ‘tired light’ models are disgraced. That was because Yakov Zel’ dovich averred that there could be no possible scattering mechanism to support a tired light model, and no one of equal import countered that we might spend a hundred years without success, looking for an explanation of the 73% of matter that no one understands. If both hypotheses had been evaluated contemporaneously, respectful comparative analyses would most likely have proceeded rather than embracing non-Copernican concepts of creatio ex nihilo, inflationary expansion at greater than light speed, a later accelerated expansion, etc, and quixotic quests to reinterpret general relativity and discover the illusive nature of dark matter and then dark energy. Quests proliferating quests. But… there it is.
We have come full circle. Initially there was Einstein’s disagreement with Newton concerning the stability of an infinite universe. Then his analogy of an expanding balloon with coins stuck on it as representative of galaxy clusters that had little to do with major cosmological issues including an origin and expansion of the universe – created and emerging from nothing. But here we are. We find that expansion is not required to keep an infinite universe from collapsing upon itself nor is it required as a cause of the observed cosmological redshift. It turns out that the hydrostatic pressure that determines thermodynamic aspects of galaxy clusters accounts also for the baryonic mass density, observed average kinetic temperature, the, average kinetic and radiation energy density, and the cosmic microwave background (CMB) that characterize the universe. It is thermodynamic analyses to a greater extent than gravitational that are required in modeling the real stationary state of our universe.
[1] A ‘stationary state’ does not imply a static or refuted ‘steady state’ model; it is a stable thermodynamic state.
Leave a Reply