Gravitational lensing smears images of more distant galaxies into crescent shapes within a few seconds of arc from the center of the lensing cluster and its own orbiting galaxies. These crescent shapes may become complete circular discs if the lensed galaxy and observer are both equidistant from the lens cluster. Knowing the approximate dimensions of clusters and their mass densities (both baryonic and dark) provides the basis for analyzing what is observed.
This bending of the propagation path of electromagnetic radiation due to the mass equivalent of the photon in the gravitational well surrounding massive bodies is accepted phenomena. It was confirmed a century ago, initially as up to 1.75 arcseconds of deflection in star maps near the limb of the sun as shown in figure 1. The formula using Einstein’s general theory predicted deflection angles of twice what would be expected from Newton’s gravitation theory. The formula is:

theta = the angle at which light is deflected
G = 6.67 x 10-8 dyne gm2 / cm2 is the gravitational constant
M = mass in grams enclosed within the radius b (spherical symmetry) of object deflecting the light
b = distance of closest approach of the light path to the center of the enclosed mass
c = 2.9979 x 1010 cm / sec is the universal speed of light through a vacuum.

Figure 1: Deflection of starlight documented by Campbell and Trumpler (1922) during a solar eclipse
The functional relationships in this formula are illustrated in the panels of figure 2. Panel 1 demonstrates the angular defection effect for light paths passing at various distances b in the vicinity of a massive region. Panel 2 illustrates the amount of deflection through the same point of closest approach for various masses M of the deflecting object.
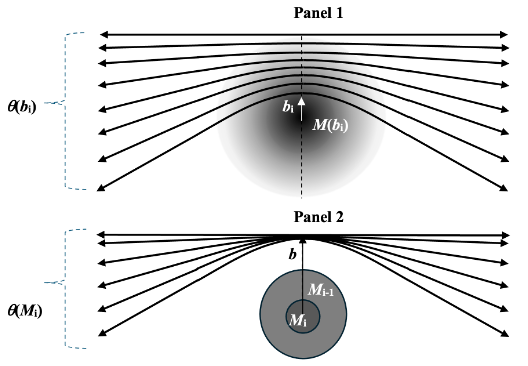
Figure 2: The amount of deflection for various values of b and M
The angles in figure 2 are exaggerated for illustration, as indeed they are in figure 1. But in the depth of space D as shown in figure 3 small angles subtend vast distances of closest approach b and galaxy clusters outweigh the solar mass by fourteen to fifteen orders of magnitude. An ‘Einstein ring’ refers to a rare occurrence of the lens focal point coincidence in which the distance of the observer is located diametrically opposite and at the same distance D from the lens object as the object being observed through the lens. This is shown in figure 3.
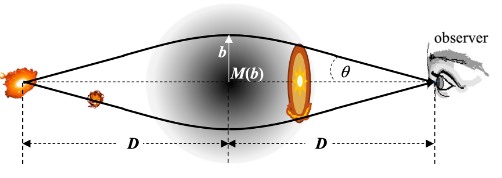
Figure 3: Geometric coincidences precipitating the observation of an Einstein ring
Here are some example predictions of lens objects and their masses, the distances of the observed object and observer from the lens object, and associated deflection angles:
lens object solar mass distance to lens (pc) ring radius
star 1 100 0.0089
1 1,000 0.0028
1 10,000 0.00089
galaxy 1 x 1012 100 Mpc 8.9
1 x 1012 1,000 Mpc 2.9
1 x 1012 10,000 Mpc 0.89
galaxy cluster 1 x 1015 1,000 Mpc 89
1 x 1015 10,000 Mpc 28
1 x 1015 100,000 Mpc 8.9
The largest example of an Einstein ring is shown in figure 4.

Figure 4: The largest Einstein ring with a radius of about 15 seconds of arc
An observed Einstein ring phenomenon is not a ‘ding an sich’ or actual object, it is the appearance of an object like a mirage or your image in a mirror that is not confused as being your clone. So it is the situations that occur between the observer and the actual lensed galaxy that produce the illusion. So let’s consider these mechanisms.
The Einstein ring associated with galaxy cluster 022058s is about 15 arcseconds in radius. So let’s investigate the angular properties of this and other lenses. First of all, complete lenses are infrequent; one must think much less frequent than galaxy clusters of 1015 solar masses for which there is a galaxy directly behind them at approximately the distance that we as observers are from the lensing cluster. The apparent distance to the lens would have to be over 10,000 Mpc, such that with clusters averaging a diameter of about 45 Mpc, we must be looking through 220 clusters between us and the lensed galaxies. Somewhere in there, there must be a galaxy that is at the right distance from the particular cluster that will become the lens. But in passing through each one of the intermediate clusters there will be deflections of various magnitudes and directions as indicated in figure 2. So it is nearly miraculous that Einstein rings would be observed at all. So the angles and masses of clusters seem somewhat incompatible.
Everywhere in the universe excepting here within the solar system, mass has been redefined to include ‘dark matter’. So now we distinguish two kinds of mass, ‘baryonic’ and ‘dark’ that have equivalent gravitational properties, but the former is endowed with the capability of interacting electromagnetically with other baryonic atoms included in the Periodic Table. The latter, although supposedly much more abundant other places than here, has no such secondary capabilities and as such is invisible. Be that as it may, it has been convenient to consider the universe at large to possess five times as much dark matter as the stuff that is hampers us here on planet earth. This predominance demonstrates itself in virial forces that collaborate the velocity dispersion of material in giant galaxies and the galaxies themselves through galaxy clusters to account for the fingers of god phenomena as separate from cosmological redshift. The 5-to-1 ratio collaborates the presumption of the universe possessing Einstein’s ‘critical density’ by increasing the observed average baryonic mass density to account for a ‘flat universe’ that only fools us into thinking it exhibits Euclidian geometry. Okay… but we have elsewhere dismissed perceived requirements for dark matter, so what about its requirement in the lensing of distant galaxies?
If we consider only baryonic mass in Einstein’s formula, then the M in the formula must be replaced by m = M / 6 and Öm = 0.408 ÖM = 4.08 x 1014 MO, which bodes well with the 4.5 x 1014 MO for the average mass of galaxy clusters throughout the universe that we came up with in quantifying the partitions of the universe. If three of these typical clusters happen to be aligned as they will be on a determinative fraction of directions in space, the Einstein ring radius would be the same with no presumption of dark matter once again. Voila!

Figure 5: An equivalent Einstein ring radius without dark matter
Leave a Reply