As we have seen, the measured geometrical relations of observed events for two such relatively moving observers inevitably produce incongruent reports of the same events. Some sort of commensurability must be established if there is to be any possibility of achieving covariant formulations of the laws of physics. To realize this there must therefore be constructs to rectify (rather than merely ignore) geometrical disparities between observers. These have a vestigial counterpart in the special theory; in fact it was key to later use of tensors so essential to extending relativity into the general theory. But because the special theory presumes mutual orthogonality of coordinate axes, it assigns to this ‘metric’ a role no more significant than a glorified identity matrix.
We will begin by defining the ‘self metric’ that we will then extend into the ‘relative metric’.
applicability of basis vectors
Of course the establishment of a coordinate frame for the registration of events within a framework suitable for an observer to categorize locations and times of events in a systematic way is the first step to obtaining an understanding of observed phenomena. For obvious reasons this organization must involve for each tabulated event one value for each of the four recognized dimensions. These values are easiest to deal with when they reflect distances along mutually perpendicular directions. In the case of the time parameter, ‘mutually perpendicular’ takes on an only slightly altered meaning as we will see. So in four-space we establish a set of unit ‘vectors’,
where the subscript m merely indicates that this concoction is unique in defining an entire set of unit basis vectors, e4. The subscript 4 is a ‘dummy index’ used in tensor notation to indicate that all the indices 0 through 3 of the four dimensions are intended. All four of the individual unit vectors e namely e0, e1, e2, and e3 are called basis vectors because they form the basis of the coordinate system used by the observer in determining, and organizing his observation data. By convention index 0 is associated with the time value of an event which, to accommodate common units with the remaining three spatial coordinates incorporates the speed of light as ‘c t‘ where c is frequently assumed to be unity by a suitable selection of units for time. Index 1 is generally associated with the first spatial direction (usually denoted ‘x‘, which is also usually defined along the direction of relative motion); 2 with ‘y’; and 3 with ‘z’. These four ‘row vectors’ (or ‘1-forms’ as they are sometimes called) are linearly independent (i. e., none can be expressed as a linear combination of other) unit (i. e., of length one) vectors. We can organize them into a matrix array with the first row e0, the second e1, etc.. Here they are shown as separate vectors implying a matrix as follows:

In this matrix, denominated (em)n, both m and n are indices (n is not an exponent), employed in tensor-like notation. It corresponds, of course, to an identity matrix such that multiplying it times any vector yields the components of the vector in the specific coordinate system defined by the basis vectors. In this way the vector r indicating the position of an event in an observer’s reference frame could be represented as: r em º rn = (t, x, y, z), where t, x, y, and z, are the components of the vector identifying the location of an event in space and time and (em)n defines the frame of reference for which the vector applies.
An important aspect of unit basis vectors is their contribution to defining an inner product (·) of two vectors. This product is defined such that,
e0 · e0 = -1, e1 · e1 = +1, e2 · e2 = +1, and e3 · e3 = +1.
Clearly time demands its own only slightly different treatment. Notice in particular that,
em · en = 0, if m (not equal to) n.
Collectively, these conditions define what is called the self metric,
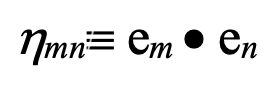
more readily visualized as:
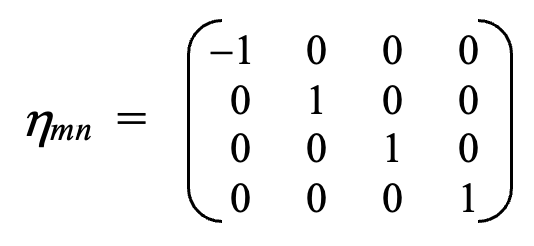
The conditions embodied in the self metric specify an observer’s geometrical situation – each of his own coordinate axes being orthogonal to every other, etc.. These values would not apply with regard to the axes of another observer in relative motion.
What is the relative metric?
The self-metric does not apply to any other observer in relative motion who assumes unique geometrical relations for which mutual orthogonality is not realized. In rigorous formalities employing Einstein’s notation the ‘spacetime metric’, gmn (analogous to a self metric hmn defined above) is co-defined with the spacetime interval in generalizing relativity, as follows:
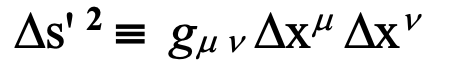
using tensor notation where again summing over common upper and lower indices is assumed. However, in Einstein’s special relativity uniformly moving observers are assumed to share a common ‘flat’ spacetime metric hm n with mutually aligned axes, whereas observational relativity must absorb observed geometrical differences into a more generalized metric similar to gm n instead – very much as Einstein did much later in generalizing relativity. Formally this relative metric is called into play in both theories to express covariant physical laws in tensor notation such as those involving an electromagnetic ‘field strength tensor’ in generalizing electrodynamics. It is used in defining a covariant derivative, and to ‘raise’ and ‘lower’ indices as a part of manipulating tensor constructs, etc.. This relative metric is determined to be:

So insisting on observational aspects of relativity has not forced us to reject either covariance or generalization, but merely to address these concepts more rigorously at an earlier stage of generalization. In fact this alternative approach embraces them in a more direct and legitimate way by employing a non-trivial metric and its inverse for all relative motion.
But first we must address the role of the ‘spacetime interval’ in another post.
Leave a Reply