Cosmologists turn into intellectual pretzels when trying to explain the bifurcation of the sparse high temperature baryonic material state of the universe and the extremely low temperature thermal radiation given off as the microwave background that has a much higher energy density than would be expected by considering the kinetic energy density of the material universe if it were uniform throughout.
The pretzel is understandable in the sense that kinetic and thermal radiation energies and temperatures have always been the same in traditional thermodynamic systems. So why have they diverged for the universe as itself a thermodynamic system? The problem is to explain the anomaly as scientifically straight-forward a consequence of thermodynamics without histrionics. If it requires the universe to have miraculously sprang from nothing and ‘evolved’ into a seething hot something that eventually cooled to 3,270 K before ‘freezing in’ that kinetic temperature, while continuing to redshift the radiation emitted those long years ago… well, I guess that’s the pretzel you’re stuck with. But that is more of a Rube Goldberg mechanism than a scientific explanation. There is a straight-forward explanation that uses only the observed data of average baryonic density of the universe, the cosmic microwave background radiation temperature, and the energy density of the background radiation. That and traditional thermodynamics are all that are required. The explanation of the bifurcated state phenomena does not require a back story.
If there are layers of partial surfaces (heated screens perhaps), the thermal radiation given off by the layered structure will increase with the number of layers of screens. With enough layers of screens the structure will be the thermal equivalent of a solid surface at the temperature of the screens. Ultimately, electrons are the sources of radiation and a thin layer of free electrons in a plasma are analogous to a very porous screen. It takes many layer to constitute what can be consider a solid surface as a basis for blackbody radiation, since blackbody radiation is essentially a surface brightness phenomena. The number of layers required to produce the equivalent ‘sky cover’ of a solid surface is determined by the cross sectional area of electrons (sigma_e) times the density of the electrons (rho_e). The percentage of closure of a ‘surface’ (which is directly related to the optical distance) is given by the base of the natural logarithm raised to minus the product of electron density, sigma, and distance as follows:
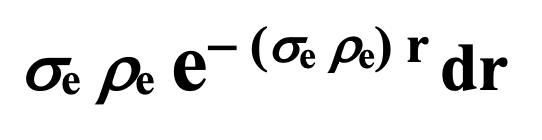
Radiation emitted from all these cross section ‘surfaces’ at increasing distances contribute to the observed radiation temperature obtained by integrating the temperature from the radiation from the partial surfaces at each distance out to infinity as follows:

Layering of surfaces to complete surface closure would not in itself produce the bifurcation of the kinetic and observed radiation temperatures — the temperatures would remain the same as shown at right.
However, in accordance with Wien’s law, the introduction of the phenomena of redshift of emitted radiation alters the resulting frequency and therefore temperature of the observed radiation without changing the blackbody form (as against the displacement) of the distribution of radiation frequency. No matter what causes redshift, Z, it is a distance related phenomena accurately represented by the base of the natural logarithm raised to the product of Hubble’s constant and distance, all minus one:
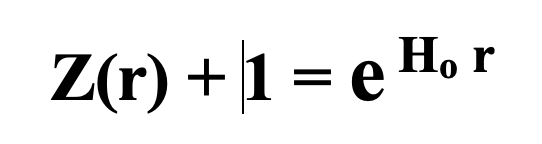
So radiation emitted from all these cross section ‘surfaces’ at increasing distances are redshifted by differing amounts to lower frequency radiation than the radiation that was emitted, lowering the temperature of the resulting blackbody radiation. The observed radiation temperature is obtained by integrating the redshifted temperature from the radiation at each at each distance out to infinity as follows:
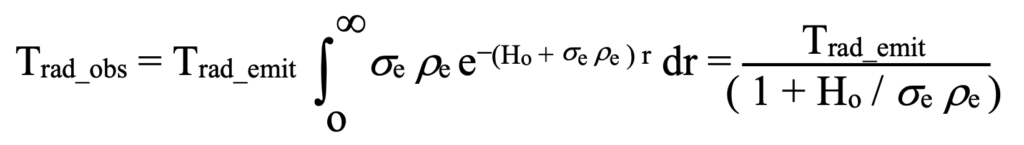
Observations tell us what we need to now about the universe today and back when the events we observe today occurred. The baryonic density of the universe is extremely low: about 10^-31 g / cm^3 implying an electron density of ~ 2 x 10^-7 cm^-3, i.e., a couple protons and electrons per cubic meter. It’s high temperature generate x-rays. And because the distance-redshift relation is a fact and not just part of a back story, thermal radiation can be observed from extreme distances for which redshift is appreciable and it accumulates to a much higher radiation energy than that produced by the low density of matter in our immediate environs. Using the observed temperature of the cosmic microwave background (CMB) we can determine the temperature at which it was emitted from all those layered partial surfaces:
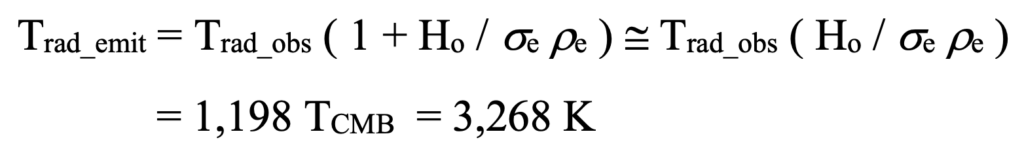
This equation is plotted below with various values of sigma. For reasons of matching the CMB energy density and because it is, in fact, the electron cross section, the value of sigma is chosen as 3.047 x 10^(-25) cm^2.
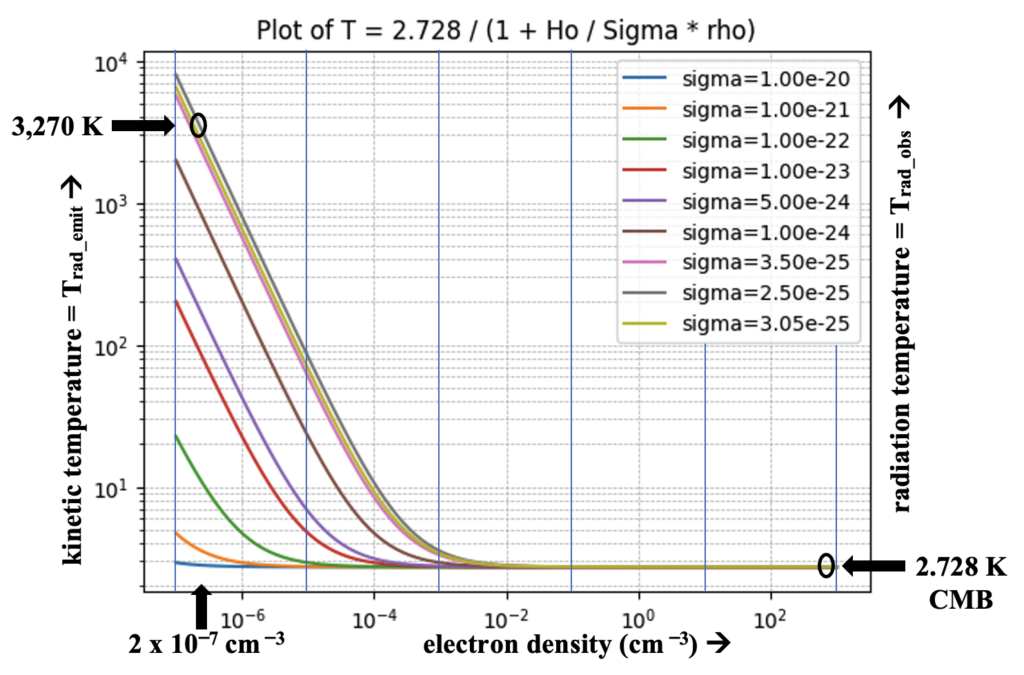
In addition to the combination of low density and redshift reducing the radiant thermal temperature, the non-uniformity of the baryonic matter in the universe accounts for the much higher than might have been expected amount of energy contained in the radiation. The equivalence of kinetic and emitted radiation energies implies the following in a system where density and temperature are evenly distributed:

Boltzmann’s constant k = 1.38 x 10^-16, so the energy expressed on the left side of this equation is 1.35 x 10^-19 erg/cm^-3 and on the right for the CMB, the radiant energy is 4.19 x 10^-13 corresponding to what is actually observed. The equivalence of the left and right sides of this equation imposes a constraint on the uniformity of kinetic temperature and density in order to guarantee T_surface = T_radiation. Thus, the CMB observations might seem to suggest (and definitely have suggested) that the electron density of the universe should be 3.1 x 10^9 times more dense than what is observed. Bringing a system into equilibrium for which the blackbody radiation distribution of T_rad is the result is what thermalization does for ordinary thermodynamic systems, but does not (or has not yet) occurred in non-uniform systems, which is why they typically do not generate blackbody spectra. But the universe does generate blackbody radiation so equilibrium is not the issue. However, the distribution of baryonic matter in the universe is non uniform because of the continual interplay between thermodynamics and gravitation that results in a cellular structure of galaxy clusters and their surrounding environs that form hydrostatically stable configurations of baryonic matter and that is the matter whose averages are representative of the averages for the universe as a whole.
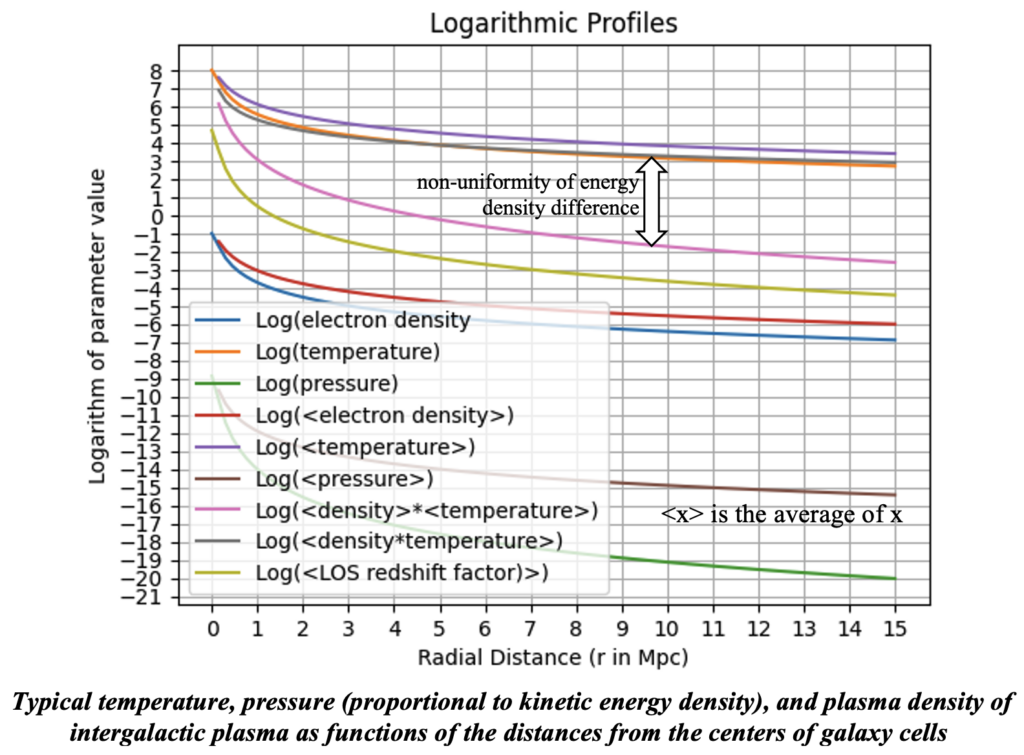
The kinetic energy density at every location of space is proportional to the pressure which is proportional to the product of the temperature and density parameter values at each location as formulated above. However, it varies considerably throughout space; the much more dense and intensely hot regions in galaxy cluster cores have substantially higher energy density than realized in the vast but sparser regions with much lower temperature and density values at large distances away from the cluster core. So averaging of parameter values is essential. We use brackets surrounding parameters to indicate an average value of a parameter x is < x >. So for the expression on the left of the equation above, for a uniformly distributed system we would have:
< E_k_ uniform > = < (3/2) k density * Temperature > = (3/2) x 1.38 x 10^-16 < density > x < Temperature > = 2.0 x 10-19 erg
Although appropriate for uniform distributions, it is incorrect for a non-uniform system. The pressure must be averaged as the indivisible unit that it is. Thus, parameter averages in the distributions applicable to representative galaxy cluster cells, the appropriate equation is:
< Ek_non-unif > = < (3/2) k pressure > = (3/2) x 1.38 x 10-16 < density · Temperature > = 4.169 x 10-13 erg
The figure below illustrates the extreme effect of non-uniformity on average kinetic energy in a representative galaxy cluster cell, a difference between < Ek_unif > that is proportional to a product of averages, < density > * < temperature > and < Ek_non_unif > that is proportional to the average of a product, < density * Temperature >. These are plotted in the figure. So clearly the average kinetic energy throughout a representative galaxy cluster cell (and by extension, throughout the universe) is not proportional to the product of the averages of electron density and kinetic temperature of the plasma but an average of the product of these parameters as the average pressure. There is a huge difference.
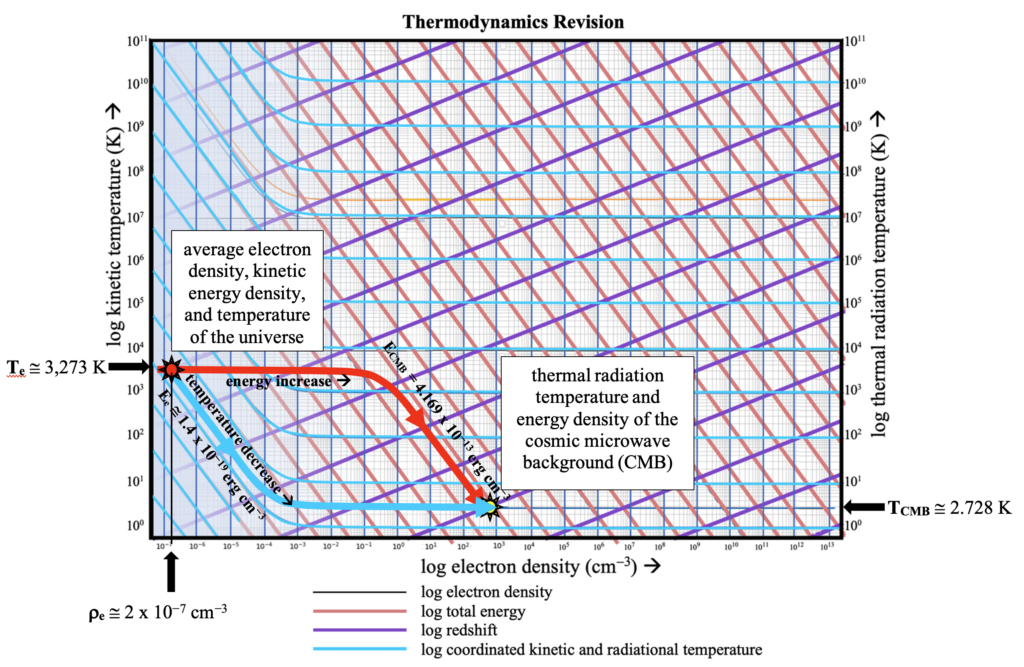
t turns out that traditional views of thermodynamic systems need to be revised when applying that discipline to the universe as a whole. If the electron density of a system is less than 10^-3 cm^-3, the system is so sparse that thermal radiation penetrates from distances for which the redshift factor is appreciable. That is why the blue lines in the figure below that connect kinetic and radiational temperature turn upwards for densities less than that. The traditional equations can (and must) be adapted, as we have above, for low densities, redshift, and non-uniformity of baryonic matter to produce the bifurcation of state parameters without narrated analogies to genesis. Four pieces of scientific data are all that were needed:
- density of the universe from which we obtain electron density
- electron cross sectional area
- CMB temperature
- CMB energy density
The rest is thermodynamics as usual.
Leave a Reply