The object of science is to design experiments or use observations of natural phenomena in a sincere attempt to refute conjectures – not to confirm them, as eloquently delineated by Popper. That is the essence of a scientific endeavor. Einstein believed the value of thought experiments. So we begin by conceiving a viability test of his special theory of relativity as representing what is observed by two relatively moving observers to attempt refutation and the improvement of his special relativity theory. Extension into the general theory will be addressed in subsequent posts.
In the parlance of relativity, we define an observer O as one who detects the locations (x, y, z) and times (t) of the occurrence of events within his ‘frame of reference’. This is a grid that is stationary with respect to the observer; it moves with him. It has calibrated distances along each of the three mutually orthogonal directions and light travel time intervals to a central ‘observer’ from each location in this space. Such detections are what we shall refer to as observations. Two observers, O and O’ synchronize their clocks and share the same unit distance values in their respective frames of reference so that their observations will be commensurable. An event is a notable occurrence at a specific time and place (t, x, y, z) within this frame of reference.
In the ‘special’ relativity that we address initially, we conceive two such observers O and O’ in uniform relative motion with respect to each other. For convenience (but no other meaningful reason) we assume that their relative motion is along their respective x axes as shown in figure 1.

Figure 1: Reference frames for observers O and O’ in relative motion v as observed by O
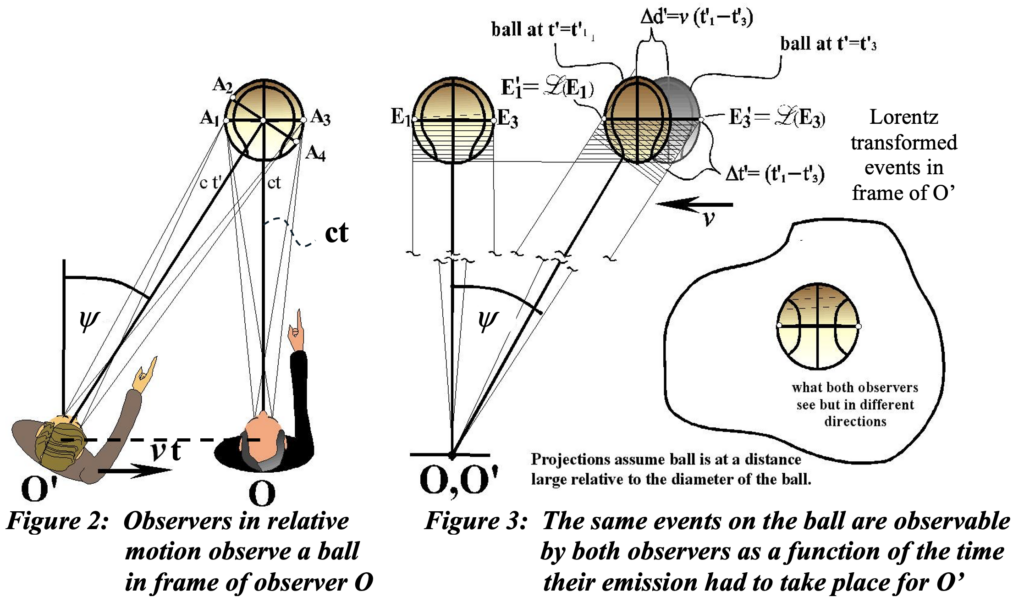
Notice that although respective x axes of the two observers are defined as being aligned, the respective y and z axes cannot be. This is because the speed of light is finite. We are dealing with observations of fleeting events E rather than rigid rods in the sense that Einstein used them in describing procedures to align coordinate axes. However, his procedure was seriously flawed and would require acceleration of one or both of the observers after assumed initial alignment. Suppose instead that each of the observers chooses to affix a rod to his y axis that is visible to his counterpart as they pass. Further suppose both O and O’ have oriented their y axes orthogonal to their x axis, pointing at a distant star whose relative motion is unknown and therefore immaterial. Thus, when each sights along the y axis, it points to the star Y or star Y’ respectively. It turns out that because of their relative motion, these stars must be unique, and when O and O’ are in coincidence and sight along each other’s y axes (‘rods’ if you like, as shown for observer O in figure 1), they observe that these axes are misaligned. His own is at right angles to their relative motion; the other is not. They do agree that the stars to which the other observer says that axis is aligned, is in fact the different star than the one to which his (or her) axis is aligned. Thus, it is observationally indisputable that their y and z axes cannot be aligned. One must deal with that – which Einstein and a century of scientists have not. This misalignment is through the relativistic aberration angle psi as shown in figures 1, 2, and 3, where sinpsi = v/c.
That Einstein could actually make a mistake has been noted before, perhaps most notably by himself concerning what he considered his most egregious error. We are dealing with a different error that was noted by Roger Penrose in a 1957 article that showed that whereas Einstein had stated that a spheroid passing by an observer would appear Lorentz contracted into an oblate (pancaked) spheroid, it would not. Penrose meticulously demonstrated that instead, neither the spheroid nor in fact any object, would appear Lorentz contracted; it would instead appear rotated through an angle psi with respect to the direction of motion. Notably, cos psi = root( 1 – v2/c2 ), that happens to be equal to the supposed Lorentz contraction factor; so a rod would look contracted.
Penrose was young at the time, and certainly not ‘Sir Roger’; perhaps that has some bearing on why he concluded that although Lorentz contraction cannot be observed, the object must most definitely be contracted, nonetheless; it just ‘appears’ not to be. But this is not Schrodinger’s cat, mind you; either it is contracted as it appears not to be, or it isn’t. To further resolve this issue, Penrose showed that the process of ‘seeing’ an object, changes what we see. He demonstrated that when we look at a contracted object, what we observe of the object has undergone a second transformation that he called the ‘transformation of the field of vision’, shown diagrammatically in figures 2 and 3. If the ball were stationary with respect to O’, the process would be reversed, but both would see the same face of the ball. It should be noted that the ball is assumed to be at a large enough distance from observer O so that angles about the center of the ball are minimal.
So, let’s think about this; it is a thought experiment, right? Observer O observes an ensemble of events – maybe the face of a clock or a basketball. To determine what O’ will observe, each event in the image must be transformed using the Lorentz equations. But we’re not done yet! Now we must reassemble the already transformed events by processing them through Penrose’s transformation as illustrated in figure 4. Penrose’s transformation is defined to convert a Lorentz transformed mapping from this observer’s ‘reality’ (that of O) into what is ‘observed’ (‘visually’, if you will) by the other observer (O’). He did this by lashing together a second transformation that would take the result of what theorists (and Einstein himself) had for half a century held to be sufficient in and of itself to accommodate what would actually be observed by a second observer.
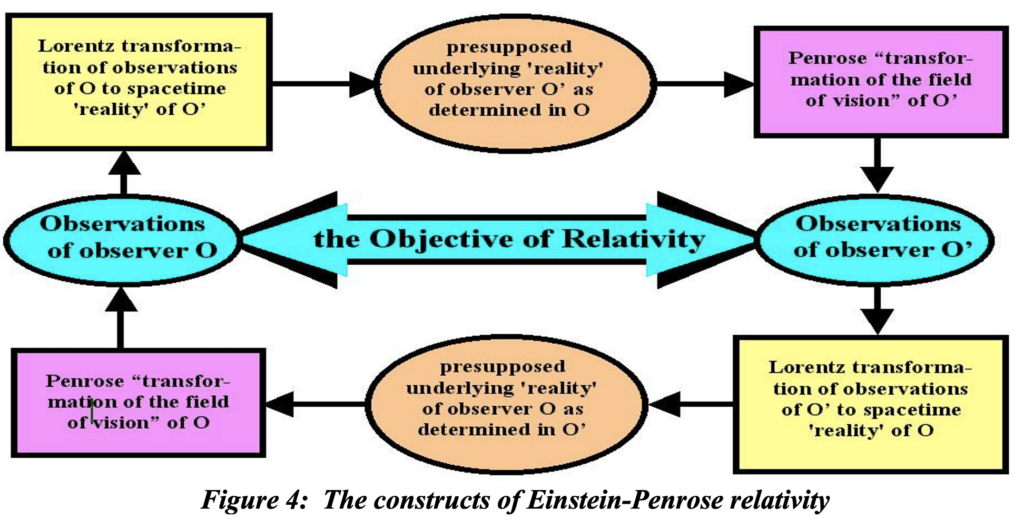
Who decided that science is about a non-observable reality? I didn’t; I don’t. The extent to which one’s reality differs from what is observed is a measure of the extent of one’s insanity or of being unscientific at the very least. Is there any meaningful purpose in promoting underlying realities to which Lorentz contraction and time dilation actually occur if they cannot be observed. I say no. Instead of successive transformations there must be a transformation of observations shown in figure 5, that deals with coordinating observable realities, i.e., their frames of reference.
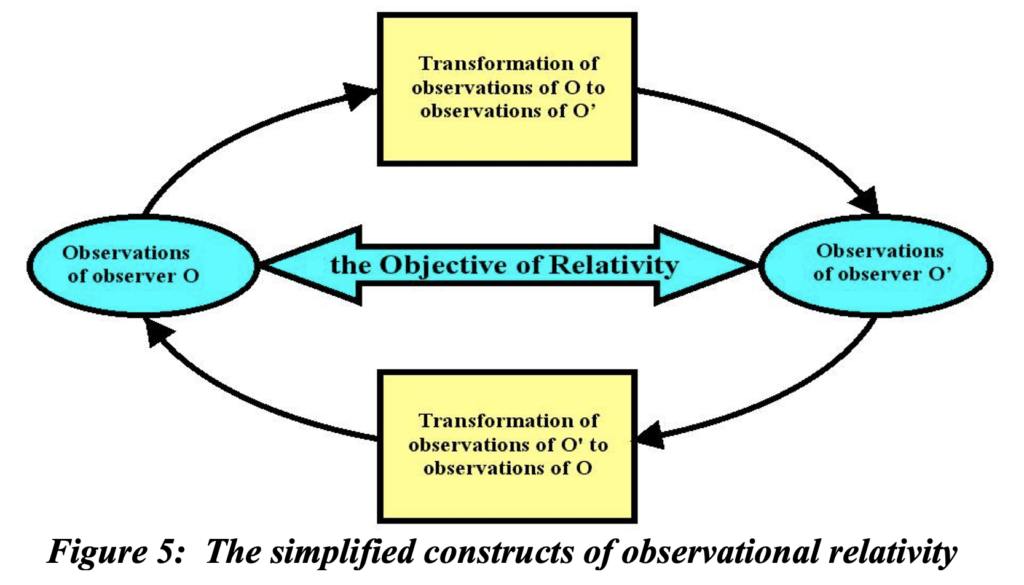
What we are trying to find is the formulation of this Transformation of Observations. And in that endeavor, let’s look at figure 2 and reconsider a willingness to embrace time dilation. This figure is drawn from the perspective of O. So the time t involved in distance determinations v t and c t that accurately reflect where an observer O’ had been situated when events on the center of the face of the ball took place in the reference frame of O. Both observers can observe the same ball when they are in coincidence( refer to the previous post on frame independence), the transmission time must be identical for both of them as described and illustrated in that post. So not only is the appearance of the ball rotated through the angle y, but lines of sight to the center of the observed face of the ball as seen by O’ are also rotated. Instead of a ball, now envision a wall clock at the distance c t, an amount of time shown on clocks in figure 6 as one hour.
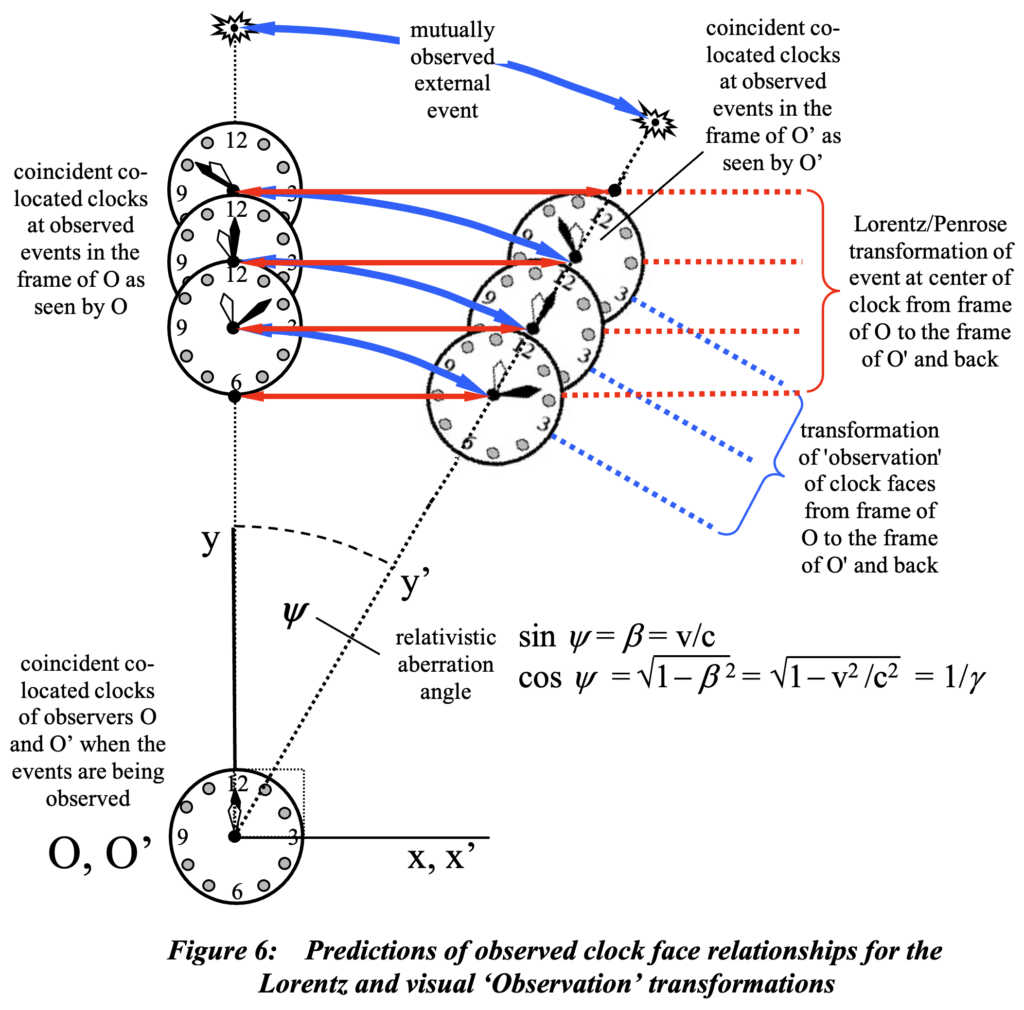
The fact that both observers see the same face of the ball or face of a clock at the same time, while in coincidence, implies that there is neither contraction nor time dilation involved between the observations in different frames of reference. The only difference is the aberration angle between observations. Notice the time displayed on the clock when each event occurred. The only observed difference is a complete rotation of the angle at which it is seen, matching the orientation through the angle psi. The trigonometric properties of this angle are the following:
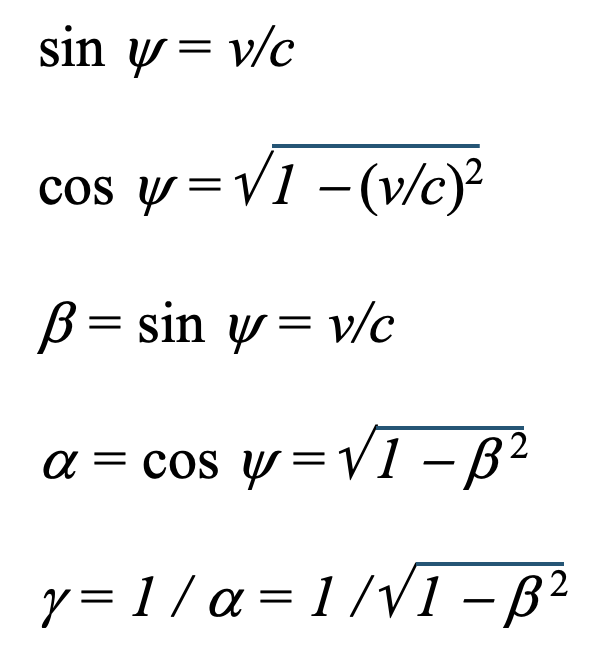
But whatever the differences and similarities of the Lorentz and Observation transformations, they belong to a class that supports covariance of physical laws. Features of the transformations were illustrated in figure 6; a Lorentz transformation is a skew rotation, whereas the Observation transformation is a simple rotation, both through the angle psi . The equations that transform the event (t, x, y, z) in the frame of observer O into (t’, x’, y’, z’) in the frame of observer O’ for each transformation type is provided below where a plus or minus, (± alternative) sign apply depending on whether the other observer is proceeding in the positive or negative x direction.

The profound implications of acknowledging this necessary change in the perspective of the relationship of observations made by observers in different dynamic situations will be addressed in subsequent posts.
Leave a Reply