I need not try to convince you that old men live in the past and too often repeat anecdotes they see as too precious not to be re-expressed. Not that I am such an old man, but I guess I tend to see aspects of reliving the past more as a feature rather than a flaw. Sort of a ‘deja vue all over again’ phenomena. As excuse, let me just say that facebook keeps asking me, “What’s on your mind, Fred?” and priming the metaphorical pump (an allusion with which most will not associate) with what happened to be on my mind years in the past — like, “Here is what happened two years ago.” So there’s that.
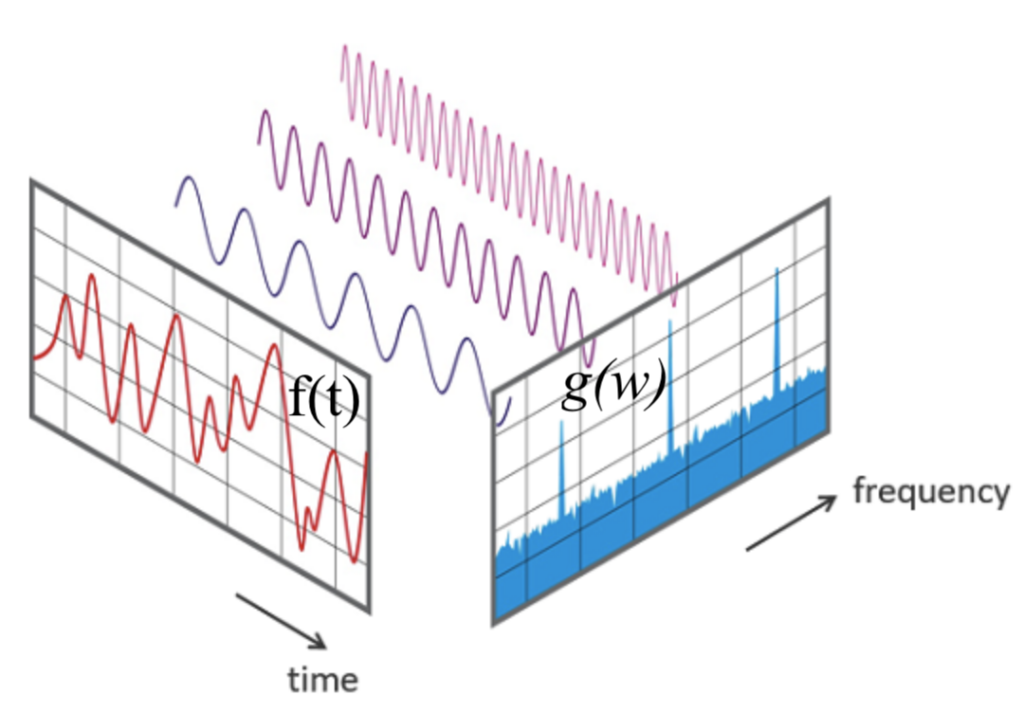
Today being the two year anniversary of one of those precious anecdotes recited on facebook provides the opportunity to correct and amend earlier comments. Two years ago I found a hand-written note I had written in October 1967. So today I’m face-to-face with it again and feel compelled to clarify some of its obscurity. I obviously referred to the Laplace Transform rather than the Fourier Transform because the concept I was addressing applies to all space and time, not just finite intervals of both. But the concept is very similar as illustrated by diagram I found on the internet that applies specifically to the Fourier transform.
I have taken the liberty of editing what I wrote 56 years ago to make it more readable, but the notion in the original I have left unchanged although I see it as having additional application to the Mind vs. Body problem. I have also allowed myself to look up and read about Geulincx (which was noted in the left margin of the original as something I happened to have read two days after having written the original note) and his related ideas including ‘occasionalism’.
So here is the newest edition of the old man’s story, followed by the original from all those years ago.
————————-
On Free Will vs. Predestination
Oct. 14, 1967
In connection with the paradox of Free Will vs. Predestination, the application of mathematical relations used in analyses in physics known as the Laplace Transform is of interest. The method involves the transforming a physical problem into an equivalent form involving a totally different variable for which solutions may be intuitive or easier to obtain.
If, for example, at time t_0 a switch is thrown in an electric circuit (or virtually any act that initiates some temporal behavior) resulting in a current flowing with some arbitrary non-zero functional form f(t) only after the switch is thrown, then the function can be written as the integral of another function of a different variable that is invariant, existing as a non-trivial function from minus infinity to plus infinity of that variable. Thus, the function can be expressed as:
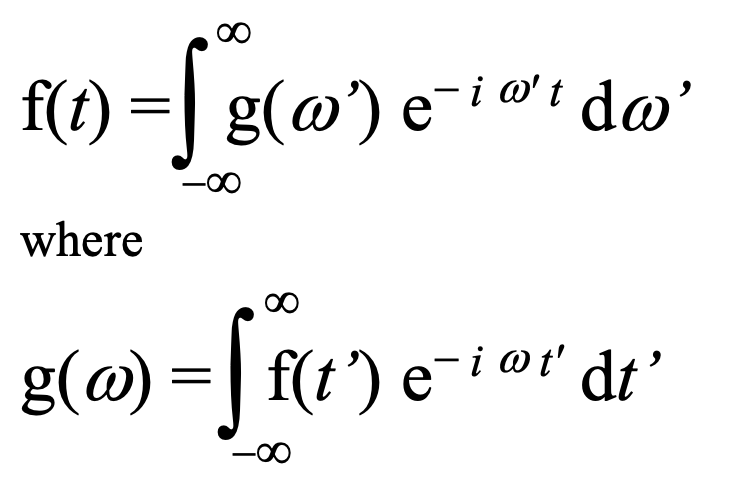
The g(w) are traveling waves of pure frequencies existing unchanged for all time. (See diagram above.)
To understand the functionality of the integrands in these equations, one needs to understand a bit about ‘complex’ numbers, i. e., numbers that have both a ‘real’ and an ‘imaginary’ part. These are treated as two-dimensional (vector type) numbers in a plane. The unit complex plane is defined by e^(i *theta) = cos theta + i sin theta , where theta is an angle, i = sqrt( – 1), and w t = theta(t) is an angle that increases with time as shown below.
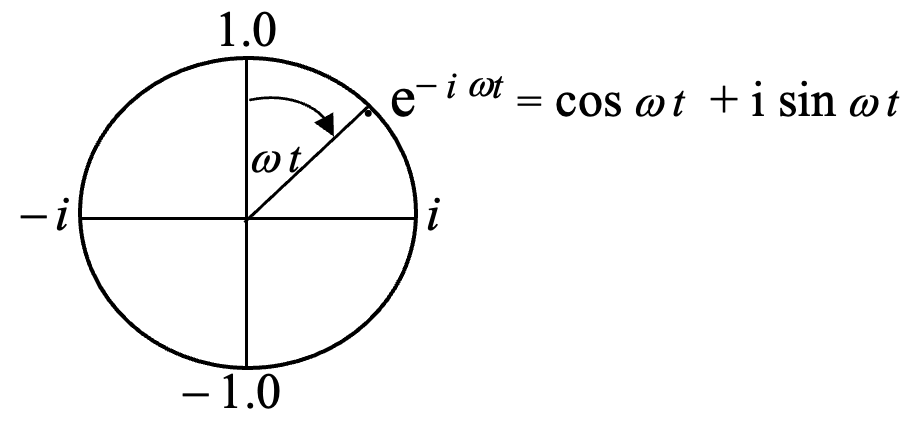
Then with the imaginary plane perpendicular to the plane of the page, the plots are projections of the integrands of the two integrals :

Thus, for each value of w’ there is an infinitely long sinusoidal function. All of these that in total comprise g(w) are added by the integration step and similarly for f(t). So typically a function of finite duration is equivalent to the summation of sinusoids of infinite duration.
The following example illustrates how a series of infinite duration sinusoids approximates the function that exists only over a short interval of time. As the range of frequencies increases, the fidelity of the approximation increases.
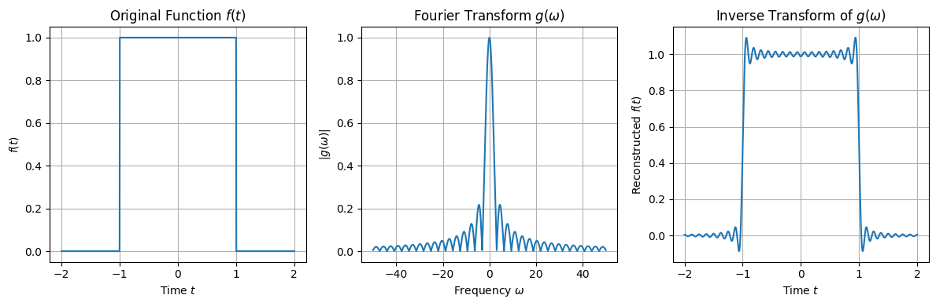
And thus it appears that the initiation of f(t) at time t_0 = -1.0 seconds determined (or was it determined by?) the existence of the eternally unchanging waves whose collective magnitude is given by g(w). The alternative hypothesis would be that the unchanging frequencies — the essence of the function f(t) — necessitated the throwing of a switch or whatever action we choose to believe initiates some ensuing functionality. Of course the motion of an arm in throwing a switch can be represented by a mathematical function of time, and that too can be expressed as an inevitability anticipated by the very nature of things for all time past, present, and future. The entire universe, if it were created or if it just happened to come into being at a particular point in time, and its functional behavior in space and time must in some sense have existed for all time even if before and after certain times there is nothing at all. Even a god, however omniscient and omnipotent must face this paradox of free will unless he, she, or it could be satisfied with being the essence of all things.
Now, without further adieu, I give you me of 56 years ago.

Leave a Reply