It was stated earlier that Einstein’s insistence on an archaic notion of the law of transmission of light that was nothing more or less than common sense at the time, constrained his interpretation of the Lorentz transformation equations – determinism being the inevitable result. Let’s consider this:
Suppose that we (K) are coincident with another observer K’ who is moving at the velocity b = 0.1 in units of c with respect to us in frame K. And let’s suppose further that there are stars or other sources of radiation observable from a distance, and that these sources have random velocities that are as high as half the speed of light. To coordinate observations with K’ we employ the relativistic aberration formula derived directly from the Lorentz’s equations:
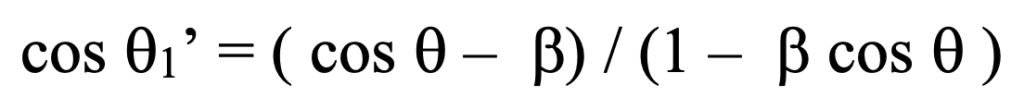
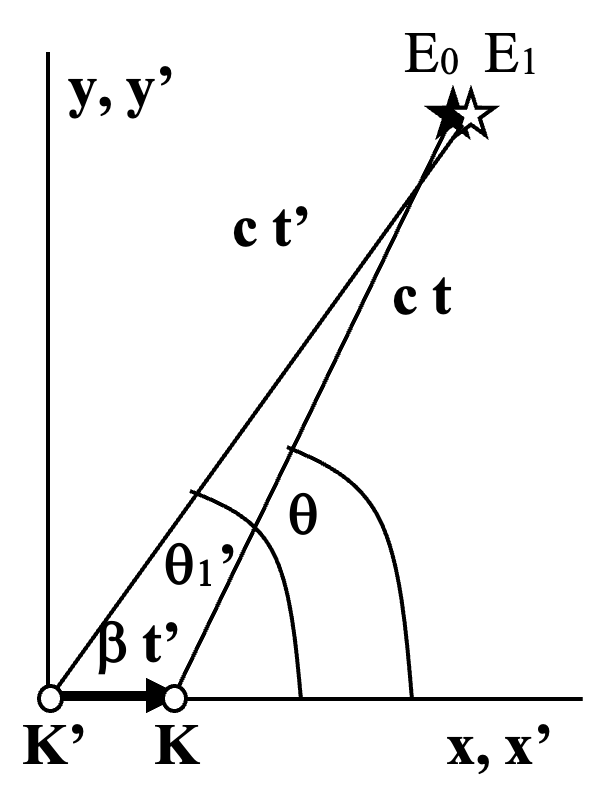
Notice in the figure that lines c t’, c t, and beta t’ do not form a triangle. (At least formally there are two events.) The deviation between angles is:
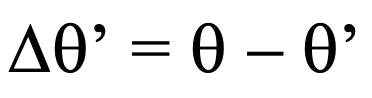
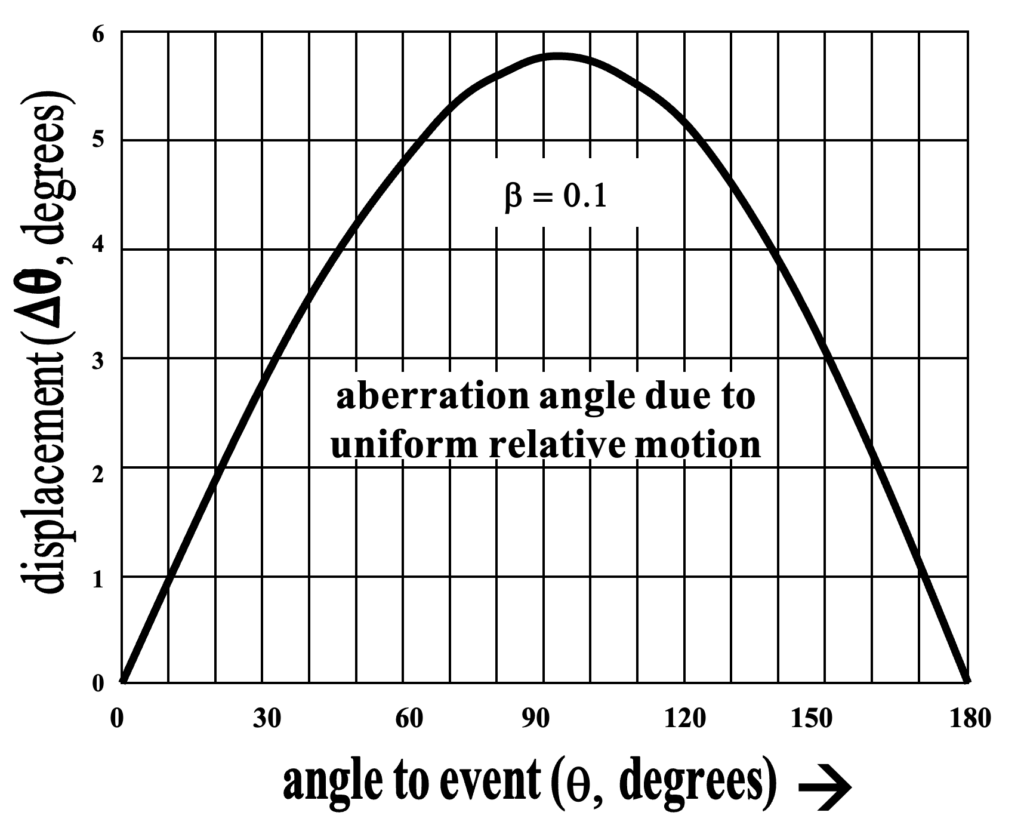
The extent of this deviation is plotted as the curve below that shows the amount of aberration between the two observers’ observations as a function of the angle theta of the observation with respect to the direction of their relative motion. Whereas with only twice earth’s orbital velocity the aberration would reach merely 41 arc seconds, with beta = 0.1, it is nearly six degrees. But other than the differences across a field of view, this can easily (and deterministically) be compensated. But with regard to events on objects moving relative to both observers what is the situation?
Let us consider light from an event on an object whose velocity is B = o.5 relative to us in K and along the direction of our relative velocity with K’. And suppose that there is an observer K” – stationary with respect to that object who just happens to be coincident with K and K’ at the moment all make their observations for comparison. NOTE: In the text expressions, q is meant to be the Greek theta.) K” sees the event at q”, as shown below. K will see the same event at the angle q given by the following:
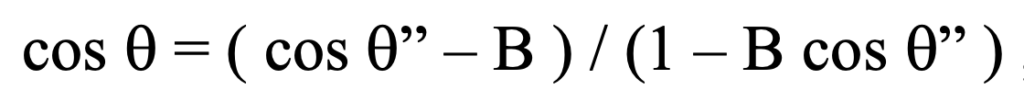
and likewise, therefore, we have:
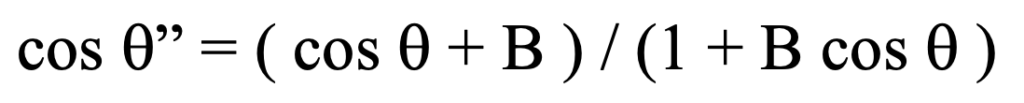

We wish now to determine where such an event will appear for K’ who happens at that instant to be coincident with both K” and K when they observe the event. To accomplish this goal of third-party coordination according to the established theory, the following relativistic velocity addition formula (what is called ‘boosting’) must be employed:
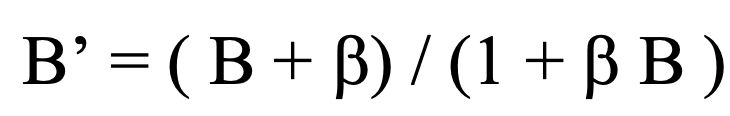
By substitution we obtain:
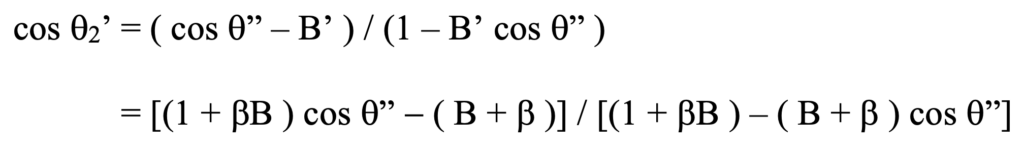

To assess how this affects the displacement of events from the perspective of K’ corresponding to event transformations from our relatively stationary apparatus, q1, we must substitute now for cos q” from the equation above, so that now we obtain the following:

By carrying out the operations indicated and canceling factors we find:
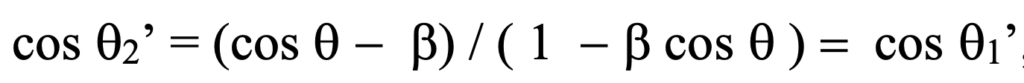
which is independent of B, such that the very same angle results between K’ and K in both cases, which is rather amazing if you think about it – or I guess more assuredly, if you don’t. As shown in the figure above the events labeled E1 and E2, which are at least by formality treated as separate events, are situated to the right and left of E0 respectively, and yet all three are hereby said to be at the very same angle for K’ no matter how this defies depiction as per the Lorentz equations.
It is very obvious why in all cases it turns out this way. According to the common sense notion embodied in the law of transmission of light, whatever anyone sees at a point in spacetime any coincident observer should also be able to see so that all events seen while in coincidence are mutually shared. (The velocity addition formula guarantees this will be the case.) ‘Seeing’ just involves photons, after all, that happen to hit one observer in the eye rather than another coincident observer…right? Well, light doesn’t work that way (see the earlier post on frame independence), but pursuing this as though we do, we find that the velocity addition formula is shorthand for a cascading of the Lorentz equations to substantiate the claim that they form a ‘transformation group’. The logic behind this accepted approach to coordination of observations is as follows:
If we let L(e) indicate the Lorentz transformation of event, e, such that:
(t’, x’, y’, z’) = L b (t, x, y, z)
and
(t, x, y, z) = LB (t”, x”, y”, z”),
then, does that imply:
(t’, x’, y’, z’) = L b (L B (t”, x”, y”, z”))
or not? That is the question. If so, it would make sense to define:
L B’ = L b ( L B),
which implies:
B’ = ( B + b ) / (1 + b B )
as used above.
With this accepted logic there can be no basis in the established theory for any uncertainty in predicted angular positions of events in space no matter what the unknown and unknowable variations in the velocities of the objects on which the events arise. The velocity addition formula distorts all space and time to collapse separate events E0, E1 and E2 to the net effect of preserving determinism.
But what – other than an archaic notion of ‘common sense’ and expediency – necessitated that the Lorentz relationships must constitute a coordinate ‘transformation’ rather than a mere correspondence? The answer is: Nothing!
All this abracadabra is unnecessary if we free ourselves from the notion that frame independence of events and mutual observability of those events cannot both apply to the same transactions between an event and its observation. Certainly whatever one observer sees can be seen by a coincident relatively moving observer, but the event that is so-observed will not have been coincident with an event mutually observed at another time and place.
Leave a Reply