
Einstein was uncomfortable with notions associated with an inherent uncertainty implied by the Copenhagen Interpretation of quantum mechanics. Whether we ourselves might ever know the precise locations and/or momenta of particular particles at particular moments in time, Einstein had faith that at least God had reason to know such things. Far from this revealing an unwavering belief in an omniscient personal savior, it merely expressed the metaphysical perspective that everything has to be somewhere, whether we know it or not! And I guess we must grant some, even if minimal, credulity to that presumption.
This insistence on knowledge of the way things are – as against what is measured or observed – came increasingly to haunt his work and that of the many dedicated theorists who have religiously pursued those paradigms Einstein established. The Great Divide between two major branches of physics – on both sides of which Einstein’s influence was monumental – involves this very issue. He opted in favor of determinism early on in his work with relativity, although his initial philosophical leanings seemed more definitely positivistic. Those early tendencies are revealed by comments such as, “we entirely shun the vague word ‘space,’ of which we must honestly acknowledge, we cannot form the slightest conception, and we replace it by ‘motion relative to a practically rigid body of reference’.” He had also indicated that spacetime coordinate magnitudes should be regarded as though the actual “results of physical measurements.” But in interpreting values that result from the Lorentz transformation equations – the formal basis of his theory that he had thus insisted be directly measurable – he failed to question all of the common sense notions of his time. Valid explanations of ‘double slit’ and other high profile experiments and related phenomena that assure us that light is anything but common sense, were unknown when Einstein coined his phrase “the law of transmission of light” for this common sense notion that even a photon must be somewhere. But we know they are not some particular where! They seem, in fact, to be nowhere until and unless they are observed. But this “law” was not specifically about how light is transmitted per se, but about the meaning of relativistic aberration – a legitimate hypothesis in as much as it is certainly refutable. But because it seemed merely ‘common sense,’ apparently no one ever bothered to doubt it sufficiently to attempt a refutation. But in this universe any legitimate God who could be invoked in a scientific context, blesses doubt!
Aberration caused by relative motion was a familiar phenomenon years before Einstein’s relativity came along. It is very much like parallax in which separated sightings of the same field of objects result in distortions between observers’ fields of view. The illustrations below illustrate this effect for parallax where observers have different perspectives on objects arising from differences in their viewing locations.
Parallax provides a useful analogy for explaining aberration. And it is easy to show that differences as well as similarities between parallax and aberration effects derive from the finiteness of the speed of light. Further, the fact that its speed can be considered the same (in a vacuum) for every observer accounts for relativistic aberration that differs slightly from what had been thought to be the case earlier. These facts necessitate that the distances that light travels, ct and ct’ in the first panel of the figure below, differ for two observers both for parallax and for aberration – except, of course, for the special case of an object occupying a position on the perpendicular plane bisecting their line of separation.
In the analogy of relative motion, for which relativistic aberration applies, the universality of the speed of light imposes constraints associated with the triangle K’KA, the geometric details of which define coincident observation of such relatively moving observers. Apparent differences in perspective for such coincident observers caused by their relative motion are extremely similar to those caused by a separation between relatively stationary observers since there had, in fact, to have been spatial separation between the observers at the time the observed light would have been emitted from the object. If observer K’ moves to the right in the figure with relative velocity b with respect to K such that bt’ = X, the analogous separation in a parallax situation, then the two angles q and q’ at which an object is observed will be given by the relativistic aberration formula to be discussed later. The extent of the difference between Einstein’s relativity and previous considerations involves the use of bt’ (rather than bt) to produce the relationship, i. e., it derives from Einstein’s Second Postulate.
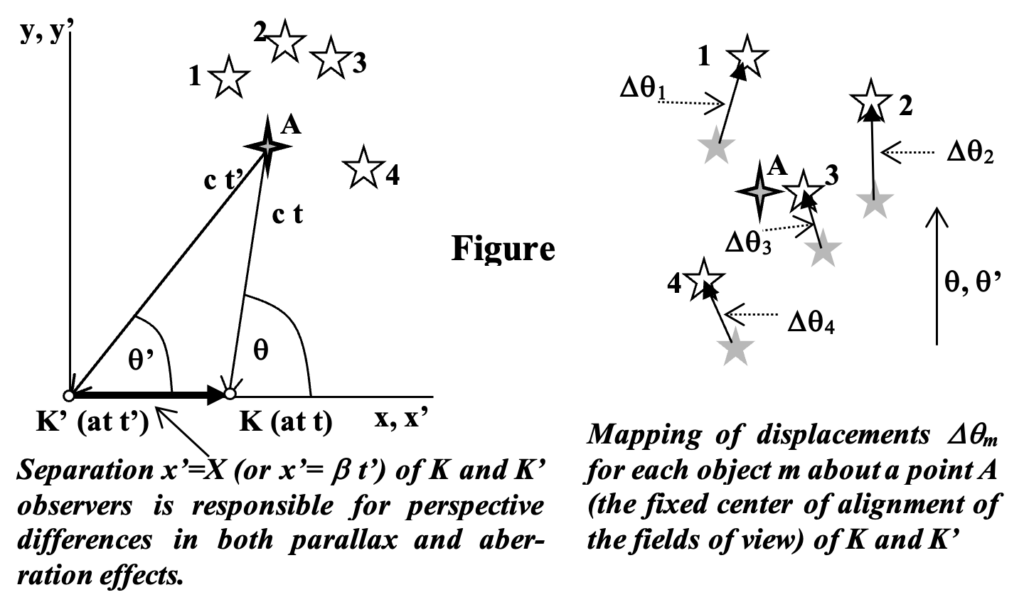
However, where there are multiple objects at various distances (and velocities) being observed, distortions resulting from parallax computations become largely unpredictable from a single observation point as shown in the second panel of the figure above. Displacements Dqm of objects within a field of view of K’ relative to where the object was viewed by K cannot be determined exclusively from angular measurements made by K of the object m. For its determination there must be some a priori knowledge of the relative distance and directional velocity of m. It is a singular fact, however, that such nondeterminism does not arise in relativistic aberration formulas when (or because) Einstein’s ‘law of the transmission of light’ is applied. Whatever is observed by K can be unilaterally transformed to obtain a corresponding observation in K’ with absolutely no knowledge of static or dynamic information of the objects being viewed relative to either observer!
Einstein’s special theory provides deterministic mappings of observations of one observer onto those of another in uniform relative motion. This is true even in cases where observations pertain to events on world lines of objects at widely varying distances and velocities. When interpreting the results of Lorentz transformations according to Einstein’s hypothesis of the law of transmission of light, all variation becomes moot. This “law” imposes an additional constraint on the Lorentz equations – namely the “velocity addition formula” – that has, of course, never been independently confirmed, or non-refuted as a scientist would prefer to say, but is a ‘necessary’ consequence of the interpretation of the Lorentz equations as a ‘transformation’ rather than as merely establishing a ‘correspondence’ between actually observed events on the world line of the same object. It is an assumption that forces an inconsistency that I think is therefore erroneous.
This piece of peripheral dogma only comes into play with regard to events on ‘third party’ platforms that would otherwise need to be mapped using direct assessments of relative velocity. What this frame independent ‘buddy system’ enforces is that the Lorentz equations produce a single coordinate direction independent of differences in the relative positions and velocities of the sources of all the events seen as occurring in this direction by one particular observer in his spacetime. That seems to the author to negate the very purpose and usefulness of relativity as a coordination (as against determination) of ‘observations’!
In ‘observing’ an event as against our merely ‘hypothesizing’ one for someone else whose composite relative spacetime situation we cannot assess – as indeed we do not even completely know our own – with regard to the source of events before the observation is made, actual observation is key. By various inferences one observer might be able to deduce from line spectra that the object has a specific radial velocity, but one still would not know its tangential velocity with any accuracy at all! The supposition that relativity can precisely transform observations made by one observer into what any other with a known relative motion (with respect to the first observer) could expect to observe – independent of the nature of what is to be observed – seems to the author patently absurd. Certainly the conjecture is refutable, and yet, refutation pends an actual two-observer observation situation, foregoing a natural urge to accept common sense notions! But first we must know what to look for, which we will address next.
Leave a Reply