To clarify the rather obtuse nature of the spacetime interval, consider that its value to every event one could ever observe is zero. A non-trivial spacetime interval is not an ‘observable’ of physics.
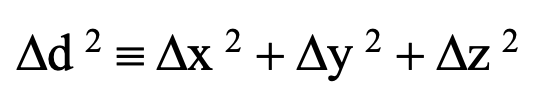
The somewhat similar path difference Ds2 (in this case defined exclusively as the squared quantity) between events in a four-dimensional spacetime continuum is defined as follows:
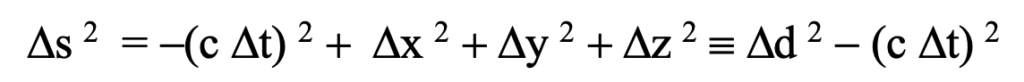
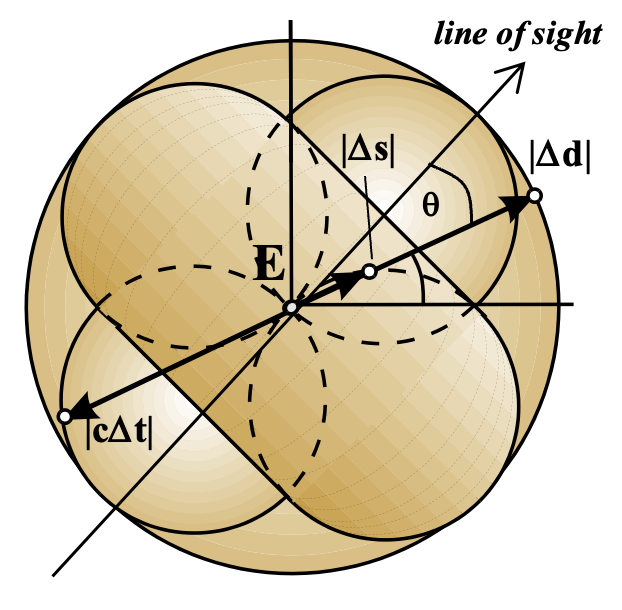
Figure: Relationships between deltas of space and tme in the spacetime interval as functions of the angle theta from the line of sight
The figure details relationships between the deltas: Ds2, Dd, and Dt. Notice that a square of the temporal difference in the occurrence times of the related events is subtracted from, rather than added to, a spatial aspect of event differences because of the convention, e0 · e0 = -1.
The universality of the speed of light c between the occurrence of an event and its observation (also an event) in each of relatively moving reference frames guarantees that the equation
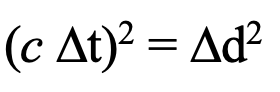
holds in both frames of reference. This is true not only of the Lorentz transformation, but also of the observation transformation as follows:
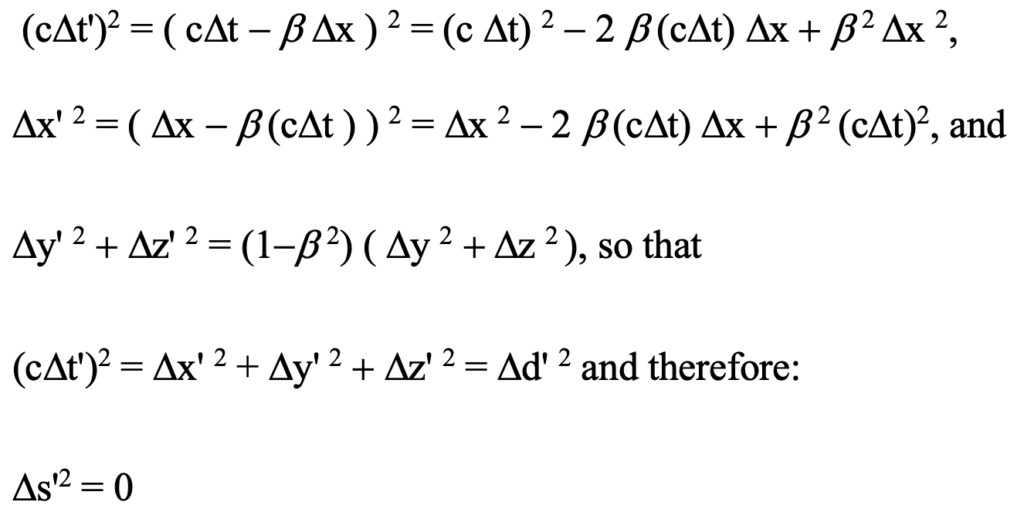
However, when we extend the meaning of Ds2 to include differences between events other than events united by emitted/detected photons along the line of sight to the observer for which Ds2 = 0, cancellation of the factor ( 1-b 2 ) in the third equation does not occur. Instead, for these situations we find that the observation transformation yields:
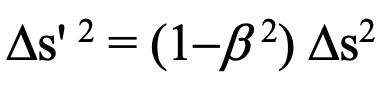
In Einstein’s special relativity the leading factor ( 1-b 2 ) is cancelled by the inverse of the factor, i.e, g 2 = 1/(1-b 2) in the Dx’2 and (cDt’)2 equations and does not exist in the Dy’2 and Dz’2 equations obtained from Lorentz transformation. So does this mean that observational relativity is thereby invalidated? No, of course not.
With regard to distant galaxies and in particular an event E associated with emission of a single photon of light that occurs in a galaxy a billion light years ago/away, one can consider the space time interval between that event and similar events that may occur in galaxies within a vicinity of E but as assessed in our personal frame of reference. Events along our same line of sight will all have spatial components of the spacetime interval canceled by the temporal components. Those at approximately right angles to our line of sight to the event E will have virtually all the spacetime interval equal to its spatial component. In short, if two events occur simultaneously for an observer (us in this case), indicating that Dt is zero, then the spacetime interval becomes just the spatial separation between the two events.
In general if |cDti| < |Ddi|, the spacetime interval will reflect the spatial difference between the events in the frame of reference of an observer for which the events occur simultaneously. Notice also that if |cDti| < |Ddi|, there can be no possible interaction between the events. And if |cDti| > |Ddi|, no observer in any frame can possibly witness the two events as occurring simultaneously. These relationships between Ds2, Dd2, and Dt2 were illustrated in the figure above for a unit spherical spatial difference about some remote observed event E. This mapping is of a sphere onto a torus as shown. Clearly, despite its usefulness in certain cases, the spacetime interval is not based on observations and is a quite non-intuitive construct.
To further clarify previous comments, observational relativity addresses the fact that uniformly moving observers do not share geometrical relations among observed events as was illustrated in previous posts. Therefore (unlike in the special theory which assumes otherwise) any metric presuming to encapsulate the geometrical aspect of respective perspectives must be unique to that particular relative motion relationship. This perspective difference of uniformly moving observers has been trivialized by characterizing a supposed mutual spacetime as merely ‘flat’. Accordingly their relative metrics were presumed to be identical with their self metrics. This is a failure to acknowledge that respective basis vectors are not (and cannot be) aligned despite continued insistence to the contrary.
Although the fact that angles to mutually observed events from coincident observation points are at an angle with regard to each other may seem to some (including Penrose, Terrell, and other pre-eminent physicists) as merely a minor embarrassment, it is however a situation of major significance. This is equally the case from a mathematical, physical, and philosophical perspective. Acknowledgment of this fact distinguishes ‘observational’ from ‘special’ relativity. But none of this precludes agreement on physical analyses of natural phenomena. Once we modify the relative metric to disavow mutual alignment, it can be used to proceed as previously.
Leave a Reply